Energy-Time Optimal Control of Wheeled Mobile Robots
Paper and Code
Jun 06, 2022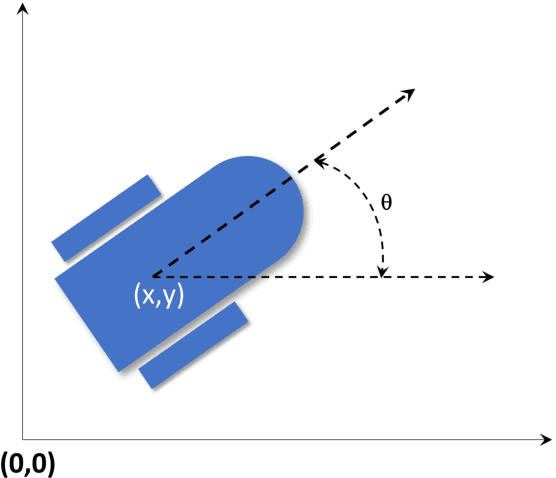
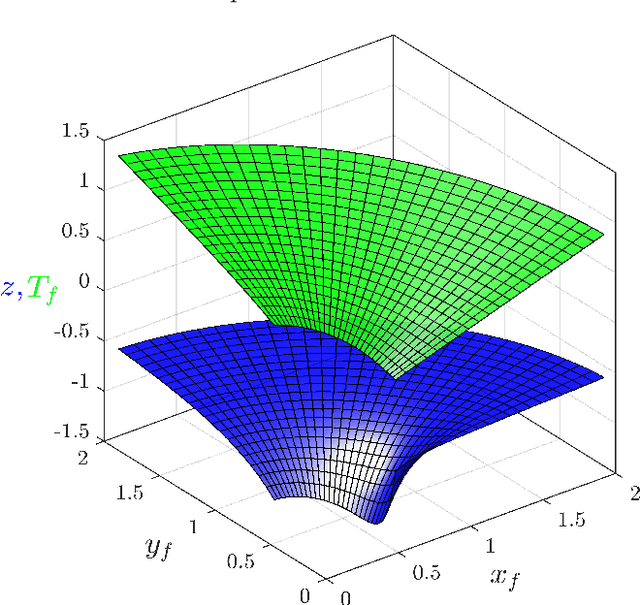
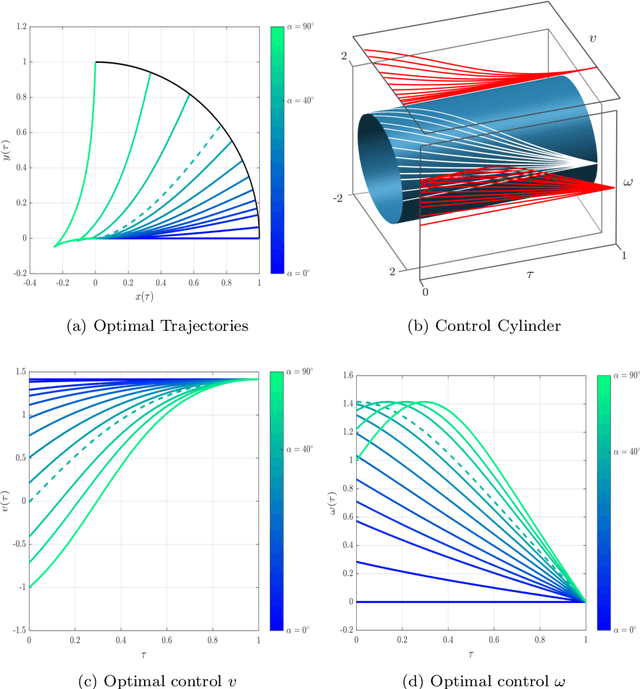
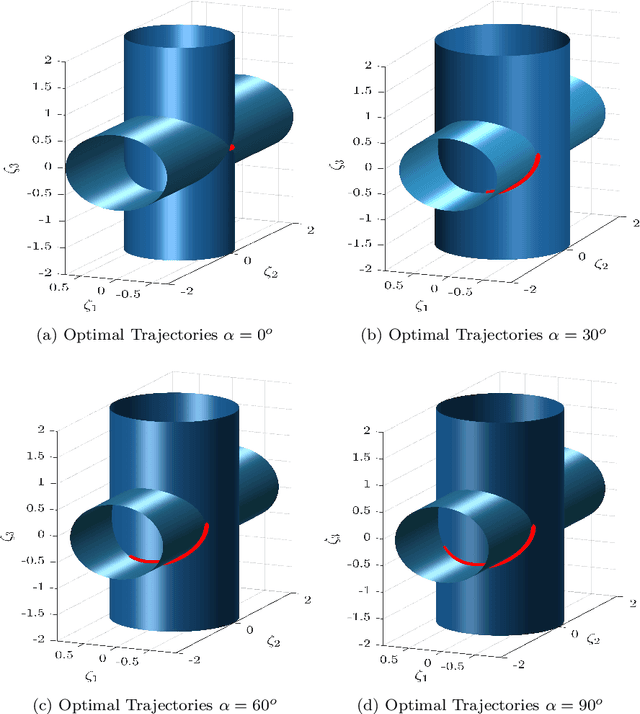
This paper focuses on the energy-time optimal control of wheeled mobile robots undergoing point-to-point transitions in an obstacles free space. Two interchangeable models are used to arrive at the necessary conditions for optimality. The first formulation exploits the Hamiltonian, while the second formulation considers the first variation of the augmented cost to derive the necessary conditions for optimality. Jacobi elliptic functions are shown to parameterize the closed form solutions for the states, control and costates. Analysis of the optimal control reveal that they are constrained to lie on a cylinder whose circular cross-section is a function of the weight penalizing the relative costs of time and energy. The evolving optimal costates for the second formulation are shown to lie on the intersection of two cylinders. The optimal control for the wheeled mobile robot undergoing point-to-point motion is also developed where the linear velocity is constrained to be time-invariant. It is shown that the costates are constrained to lie on the intersection of a cylinder and an extruded parabola. Numerical results for various point-to-point maneuvers are presented to illustrate the change in the structure of the optimal trajectories as a function of the relative location of the terminal and initial states.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge