Image registration of 2D optical thin sections in a 3D porous medium: Application to a Berea sandstone digital rock image

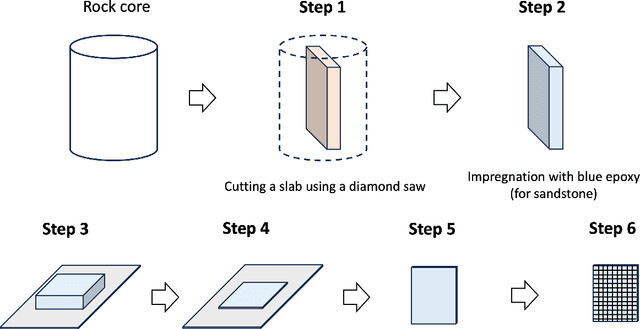
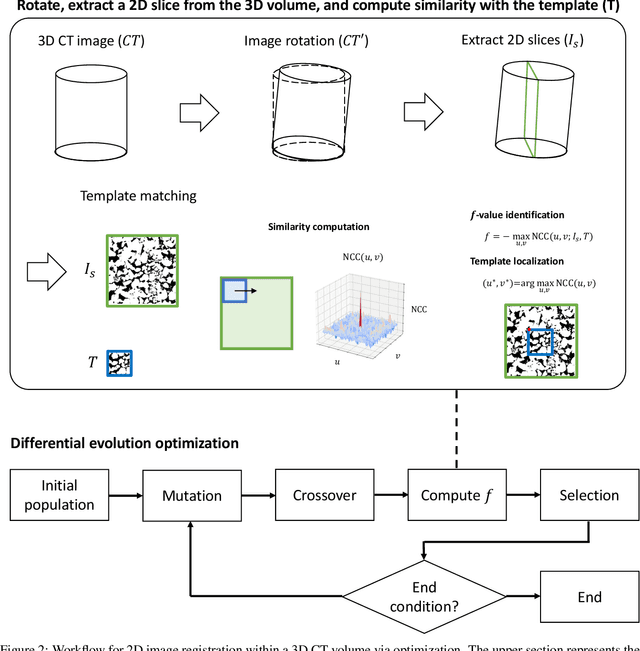
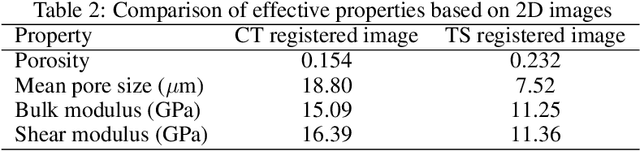
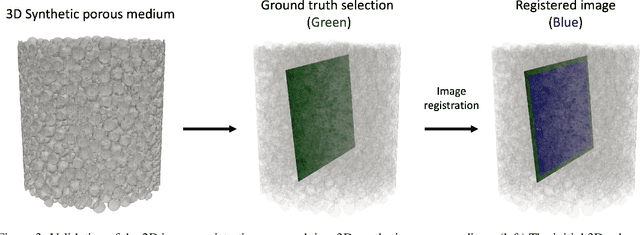
This study proposes a systematic image registration approach to align 2D optical thin-section images within a 3D digital rock volume. Using template image matching with differential evolution optimization, we identify the most similar 2D plane in 3D. The method is validated on a synthetic porous medium, achieving exact registration, and applied to Berea sandstone, where it achieves a structural similarity index (SSIM) of 0.990. With the registered images, we explore upscaling properties based on paired multimodal images, focusing on pore characteristics and effective elastic moduli. The thin-section image reveals 50 % more porosity and submicron pores than the registered CT plane. In addition, bulk and shear moduli from thin sections are 25 % and 30 % lower, respectively, than those derived from CT images. Beyond numerical comparisons, thin sections provide additional geological insights, including cementation, mineral phases, and weathering effects, which are not clear in CT images. This study demonstrates the potential of multimodal image registration to improve computed rock properties in digital rock physics by integrating complementary imaging modalities.

Physics-informed KAN PointNet: Deep learning for simultaneous solutions to inverse problems in incompressible flow on numerous irregular geometries

Kolmogorov-Arnold Networks (KANs) have gained attention as a promising alternative to traditional Multilayer Perceptrons (MLPs) for deep learning applications in computational physics, especially within the framework of physics-informed neural networks (PINNs). Physics-informed Kolmogorov-Arnold Networks (PIKANs) and their variants have been introduced and evaluated to solve inverse problems. However, similar to PINNs, current versions of PIKANs are limited to obtaining solutions for a single computational domain per training run; consequently, a new geometry requires retraining the model from scratch. Physics-informed PointNet (PIPN) was introduced to address this limitation for PINNs. In this work, we introduce physics-informed Kolmogorov-Arnold PointNet (PI-KAN-PointNet) to extend this capability to PIKANs. PI-KAN-PointNet enables the simultaneous solution of an inverse problem over multiple irregular geometries within a single training run, reducing computational costs. We construct KANs using Jacobi polynomials and investigate their performance by considering Jacobi polynomials of different degrees and types in terms of both computational cost and prediction accuracy. As a benchmark test case, we consider natural convection in a square enclosure with a cylinder, where the cylinder's shape varies across a dataset of 135 geometries. We compare the performance of PI-KAN-PointNet with that of PIPN (i.e., physics-informed PointNet with MLPs) and observe that, with approximately an equal number of trainable parameters and similar computational cost, PI-KAN-PointNet provides more accurate predictions. Finally, we explore the combination of KAN and MLP in constructing a physics-informed PointNet. Our findings indicate that a physics-informed PointNet model employing MLP layers as the encoder and KAN layers as the decoder represents the optimal configuration among all models investigated.

Seismic inversion using hybrid quantum neural networks

Quantum computing leverages qubits, exploiting superposition and entanglement to solve problems intractable for classical computers, offering significant computational advantages. Quantum machine learning (QML), which integrates quantum computing with machine learning, holds immense potential across various fields but remains largely unexplored in geosciences. However, its progress is hindered by the limitations of current NISQ hardware. To address these challenges, hybrid quantum neural networks (HQNNs) have emerged, combining quantum layers within classical neural networks to leverage the strengths of both paradigms. To the best of our knowledge, this study presents the first application of QML to subsurface imaging through the development of hybrid quantum physics-informed neural networks (HQ-PINNs) for seismic inversion. We apply the HQ-PINN framework to invert pre-stack and post-stack seismic datasets, estimating P- and S-impedances. The proposed HQ-PINN architecture follows an encoder-decoder structure, where the encoder (HQNN), processes seismic data to estimate elastic parameters, while the decoder utilizes these parameters to generate the corresponding seismic data based on geophysical relationships. The HQ-PINN model is trained by minimizing the misfit between the input and predicted seismic data generated by the decoder. We systematically evaluate various quantum layer configurations, differentiation methods, and quantum device simulators on the inversion performance, and demonstrate real-world applicability through the individual and simultaneous inversion cases of the Sleipner dataset. The HQ-PINN framework consistently and efficiently estimated accurate subsurface impedances across the synthetic and field case studies, establishing the feasibility of leveraging QML for seismic inversion, thereby paving the way for broader applications of quantum computing in geosciences.

Well log data generation and imputation using sequence-based generative adversarial networks

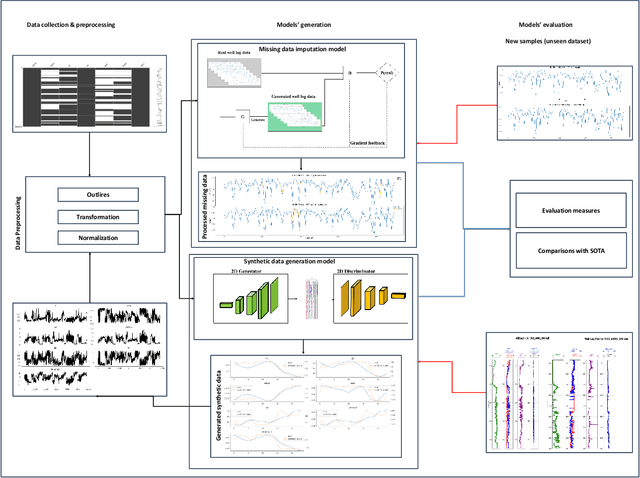
Well log analysis is crucial for hydrocarbon exploration, providing detailed insights into subsurface geological formations. However, gaps and inaccuracies in well log data, often due to equipment limitations, operational challenges, and harsh subsurface conditions, can introduce significant uncertainties in reservoir evaluation. Addressing these challenges requires effective methods for both synthetic data generation and precise imputation of missing data, ensuring data completeness and reliability. This study introduces a novel framework utilizing sequence-based generative adversarial networks (GANs) specifically designed for well log data generation and imputation. The framework integrates two distinct sequence-based GAN models: Time Series GAN (TSGAN) for generating synthetic well log data and Sequence GAN (SeqGAN) for imputing missing data. Both models were tested on a dataset from the North Sea, Netherlands region, focusing on different sections of 5, 10, and 50 data points. Experimental results demonstrate that this approach achieves superior accuracy in filling data gaps compared to other deep learning models for spatial series analysis. The method yielded R^2 values of 0.921, 0.899, and 0.594, with corresponding mean absolute percentage error (MAPE) values of 8.320, 0.005, and 151.154, and mean absolute error (MAE) values of 0.012, 0.005, and 0.032, respectively. These results set a new benchmark for data integrity and utility in geosciences, particularly in well log data analysis.

Enhanced anomaly detection in well log data through the application of ensemble GANs

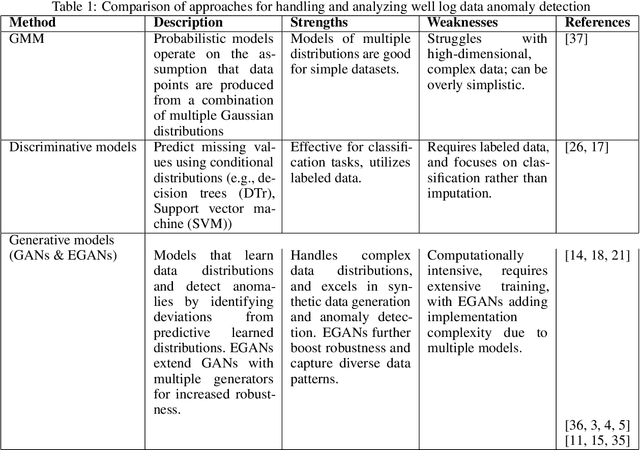
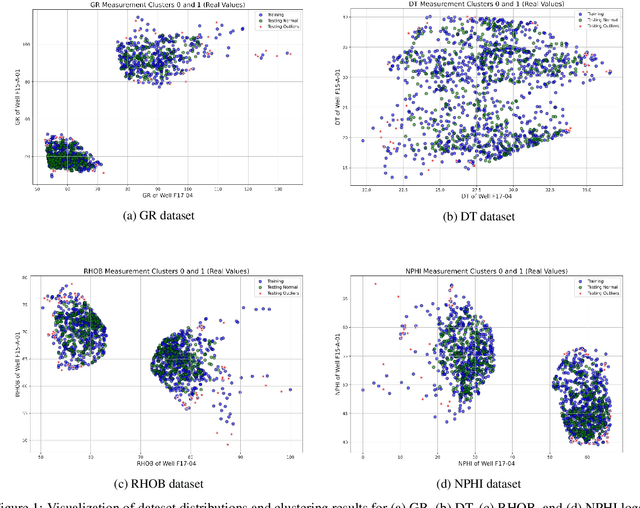
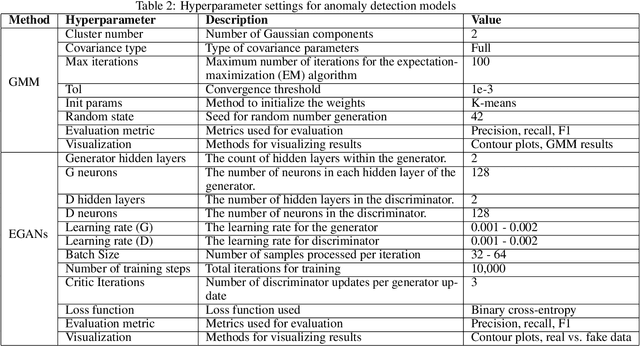
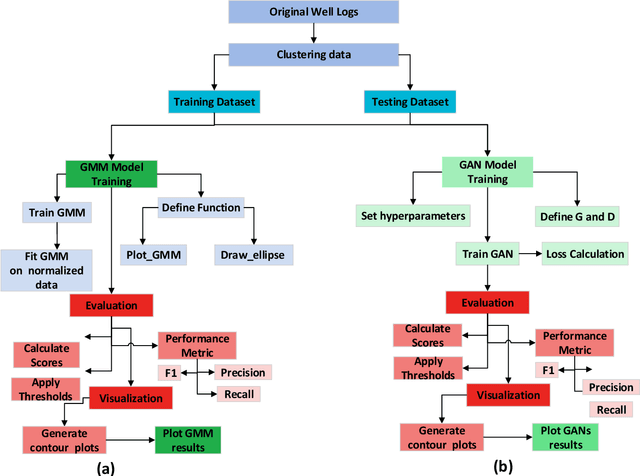
Although generative adversarial networks (GANs) have shown significant success in modeling data distributions for image datasets, their application to structured or tabular data, such as well logs, remains relatively underexplored. This study extends the ensemble GANs (EGANs) framework to capture the distribution of well log data and detect anomalies that fall outside of these distributions. The proposed approach compares the performance of traditional methods, such as Gaussian mixture models (GMMs), with EGANs in detecting anomalies outside the expected data distributions. For the gamma ray (GR) dataset, EGANs achieved a precision of 0.62 and F1 score of 0.76, outperforming GMM's precision of 0.38 and F1 score of 0.54. Similarly, for travel time (DT), EGANs achieved a precision of 0.70 and F1 score of 0.79, surpassing GMM 0.56 and 0.71. In the neutron porosity (NPHI) dataset, EGANs recorded a precision of 0.53 and F1 score of 0.68, outshining GMM 0.47 and 0.61. For the bulk density (RHOB) dataset, EGANs achieved a precision of 0.52 and an F1 score of 0.67, slightly outperforming GMM, which yielded a precision of 0.50 and an F1 score of 0.65. This work's novelty lies in applying EGANs for well log data analysis, showcasing their ability to learn data patterns and identify anomalies that deviate from them. This approach offers more reliable anomaly detection compared to traditional methods like GMM. The findings highlight the potential of EGANs in enhancing anomaly detection for well log data, delivering significant implications for optimizing drilling strategies and reservoir management through more accurate, data-driven insights into subsurface characterization.

A novel Fourier neural operator framework for classification of multi-sized images: Application to 3D digital porous media

Fourier neural operators (FNOs) are invariant with respect to the size of input images, and thus images with any size can be fed into FNO-based frameworks without any modification of network architectures, in contrast to traditional convolutional neural networks (CNNs). Leveraging the advantage of FNOs, we propose a novel deep-learning framework for classifying images with varying sizes. Particularly, we simultaneously train the proposed network on multi-sized images. As a practical application, we consider the problem of predicting the label (e.g., permeability) of three-dimensional digital porous media. To construct the framework, an intuitive approach is to connect FNO layers to a classifier using adaptive max pooling. First, we show that this approach is only effective for porous media with fixed sizes, whereas it fails for porous media of varying sizes. To overcome this limitation, we introduce our approach: instead of using adaptive max pooling, we use static max pooling with the size of channel width of FNO layers. Since the channel width of the FNO layers is independent of input image size, the introduced framework can handle multi-sized images during training. We show the effectiveness of the introduced framework and compare its performance with the intuitive approach through the example of the classification of three-dimensional digital porous media of varying sizes.

Prediction of Effective Elastic Moduli of Rocks using Graph Neural Networks

This study presents a Graph Neural Networks (GNNs)-based approach for predicting the effective elastic moduli of rocks from their digital CT-scan images. We use the Mapper algorithm to transform 3D digital rock images into graph datasets, encapsulating essential geometrical information. These graphs, after training, prove effective in predicting elastic moduli. Our GNN model shows robust predictive capabilities across various graph sizes derived from various subcube dimensions. Not only does it perform well on the test dataset, but it also maintains high prediction accuracy for unseen rocks and unexplored subcube sizes. Comparative analysis with Convolutional Neural Networks (CNNs) reveals the superior performance of GNNs in predicting unseen rock properties. Moreover, the graph representation of microstructures significantly reduces GPU memory requirements (compared to the grid representation for CNNs), enabling greater flexibility in the batch size selection. This work demonstrates the potential of GNN models in enhancing the prediction accuracy of rock properties and boosting the efficiency of digital rock analysis.

Homogenizing elastic properties of large digital rock images by combining CNN with hierarchical homogenization method

Determining effective elastic properties of rocks from their pore-scale digital images is a key goal of digital rock physics (DRP). Direct numerical simulation (DNS) of elastic behavior, however, incurs high computational cost; and surrogate machine learning (ML) model, particularly convolutional neural network (CNN), show promises to accelerate homogenization process. 3D CNN models, however, are unable to handle large images due to memory issues. To address this challenge, we propose a novel method that combines 3D CNN with hierarchical homogenization method (HHM). The surrogate 3D CNN model homogenizes only small subimages, and a DNS is used to homogenize the intermediate image obtained by assembling small subimages. The 3D CNN model is designed to output the homogenized elastic constants within the Hashin-Shtrikman (HS) bounds of the input images. The 3D CNN model is first trained on data comprising equal proportions of five sandstone (quartz mineralogy) images, and, subsequently, fine-tuned for specific rocks using transfer learning. The proposed method is applied to homogenize the rock images of size 300x300x300 and 600x600x600 voxels, and the predicted homogenized elastic moduli are shown to agree with that obtained from the brute-force DNS. The transferability of the trained 3D CNN model (using transfer learning) is further demonstrated by predicting the homogenized elastic moduli of a limestone rock with calcite mineralogy. The surrogate 3D CNN model in combination with the HHM is thus shown to be a promising tool for the homogenization of large 3D digital rock images and other random media

Physics-informed PointNet: On how many irregular geometries can it solve an inverse problem simultaneously? Application to linear elasticity

Regular physics-informed neural networks (PINNs) predict the solution of partial differential equations using sparse labeled data but only over a single domain. On the other hand, fully supervised learning models are first trained usually over a few thousand domains with known solutions (i.e., labeled data) and then predict the solution over a few hundred unseen domains. Physics-informed PointNet (PIPN) is primarily designed to fill this gap between PINNs (as weakly supervised learning models) and fully supervised learning models. In this article, we demonstrate that PIPN predicts the solution of desired partial differential equations over a few hundred domains simultaneously, while it only uses sparse labeled data. This framework benefits fast geometric designs in the industry when only sparse labeled data are available. Particularly, we show that PIPN predicts the solution of a plane stress problem over more than 500 domains with different geometries, simultaneously. Moreover, we pioneer implementing the concept of remarkable batch size (i.e., the number of geometries fed into PIPN at each sub-epoch) into PIPN. Specifically, we try batch sizes of 7, 14, 19, 38, 76, and 133. Additionally, the effect of the PIPN size, symmetric function in the PIPN architecture, and static and dynamic weights for the component of the sparse labeled data in the loss function are investigated.

ChatGPT for Programming Numerical Methods

ChatGPT is a large language model recently released by the OpenAI company. In this technical report, we explore for the first time the capability of ChatGPT for programming numerical algorithms. Specifically, we examine the capability of GhatGPT for generating codes for numerical algorithms in different programming languages, for debugging and improving written codes by users, for completing missed parts of numerical codes, rewriting available codes in other programming languages, and for parallelizing serial codes. Additionally, we assess if ChatGPT can recognize if given codes are written by humans or machines. To reach this goal, we consider a variety of mathematical problems such as the Poisson equation, the diffusion equation, the incompressible Navier-Stokes equations, compressible inviscid flow, eigenvalue problems, solving linear systems of equations, storing sparse matrices, etc. Furthermore, we exemplify scientific machine learning such as physics-informed neural networks and convolutional neural networks with applications to computational physics. Through these examples, we investigate the successes, failures, and challenges of ChatGPT. Examples of failures are producing singular matrices, operations on arrays with incompatible sizes, programming interruption for relatively long codes, etc. Our outcomes suggest that ChatGPT can successfully program numerical algorithms in different programming languages, but certain limitations and challenges exist that require further improvement of this machine learning model.