Pareto Set Prediction Assisted Bilevel Multi-objective Optimization

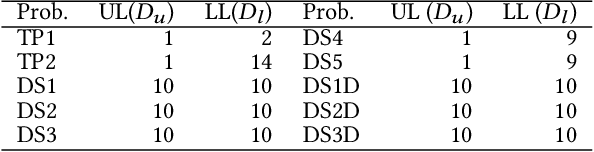
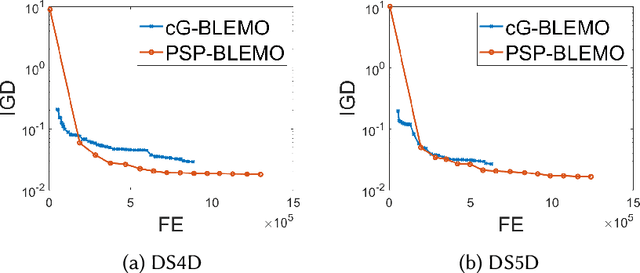
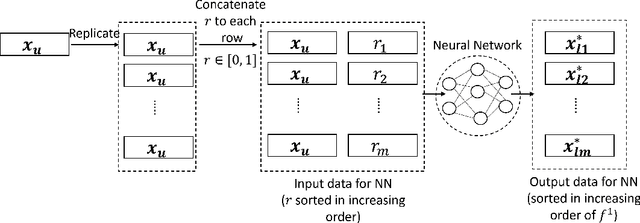
Bilevel optimization problems comprise an upper level optimization task that contains a lower level optimization task as a constraint. While there is a significant and growing literature devoted to solving bilevel problems with single objective at both levels using evolutionary computation, there is relatively scarce work done to address problems with multiple objectives (BLMOP) at both levels. For black-box BLMOPs, the existing evolutionary techniques typically utilize nested search, which in its native form consumes large number of function evaluations. In this work, we propose to reduce this expense by predicting the lower level Pareto set for a candidate upper level solution directly, instead of conducting an optimization from scratch. Such a prediction is significantly challenging for BLMOPs as it involves one-to-many mapping scenario. We resolve this bottleneck by supplementing the dataset using a helper variable and construct a neural network, which can then be trained to map the variables in a meaningful manner. Then, we embed this initialization within a bilevel optimization framework, termed Pareto set prediction assisted evolutionary bilevel multi-objective optimization (PSP-BLEMO). Systematic experiments with existing state-of-the-art methods are presented to demonstrate its benefit. The experiments show that the proposed approach is competitive across a range of problems, including both deceptive and non-deceptive problems

A Simple Evolutionary Algorithm for Multi-modal Multi-objective Optimization

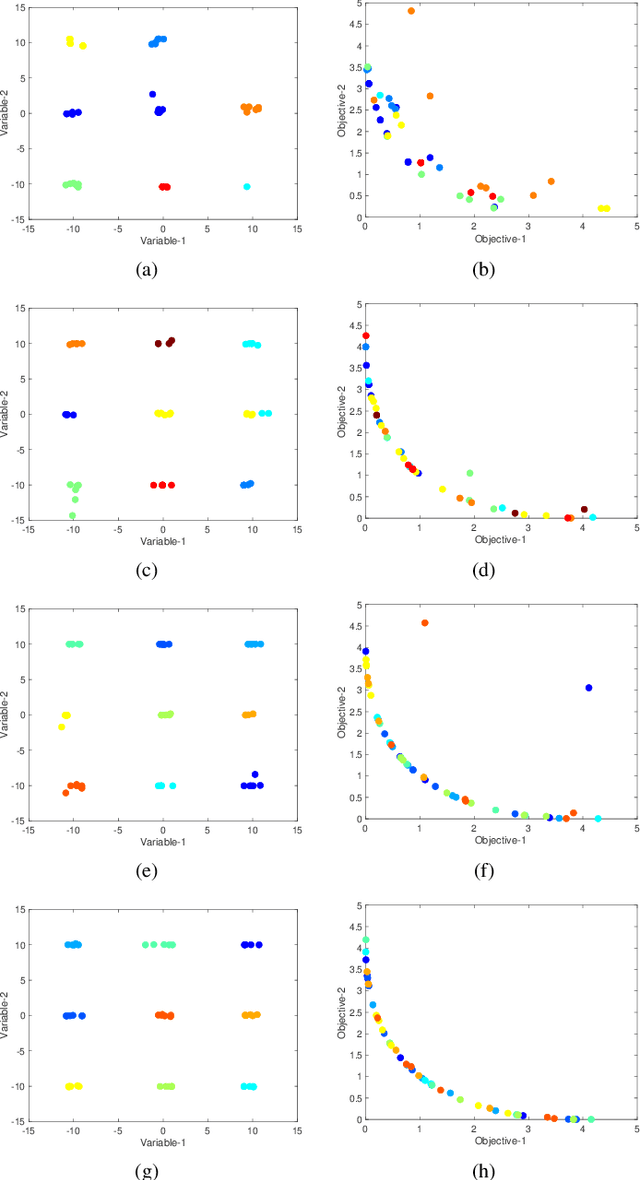
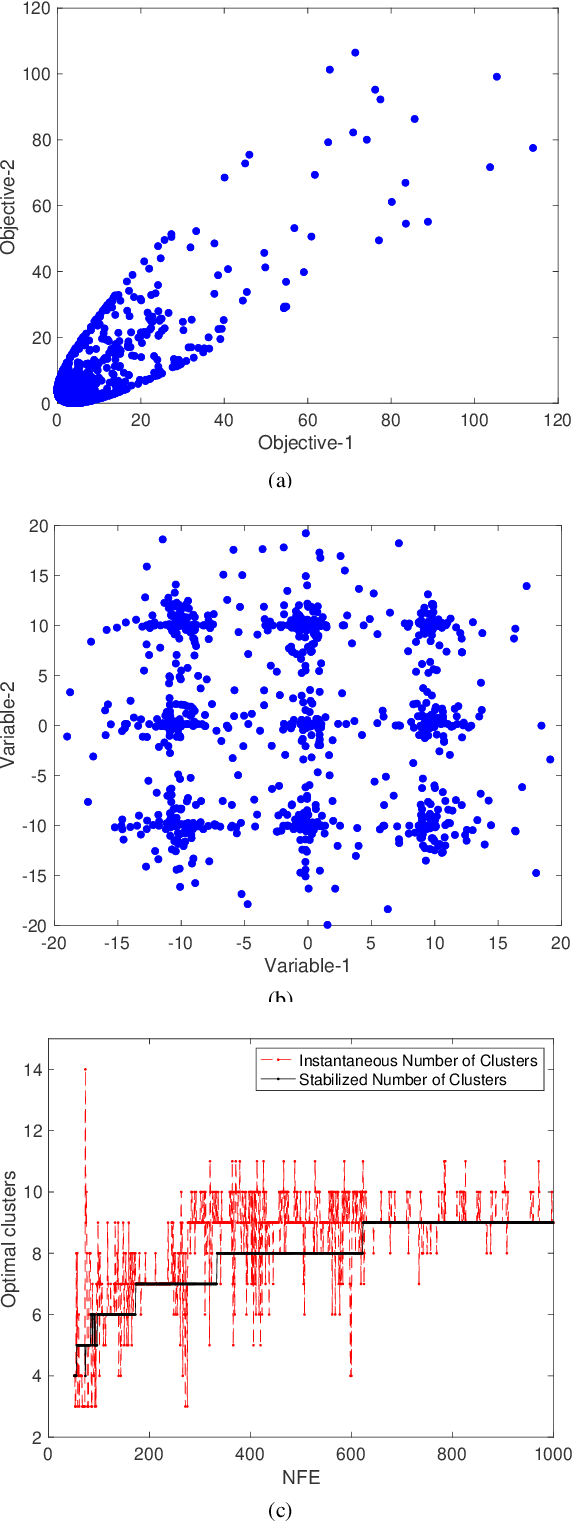
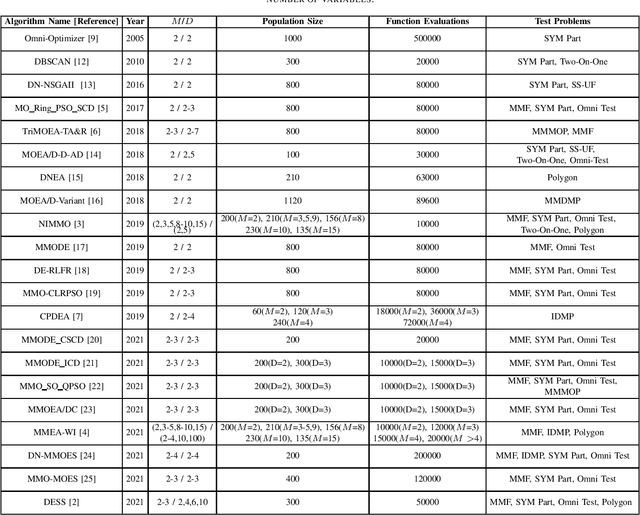
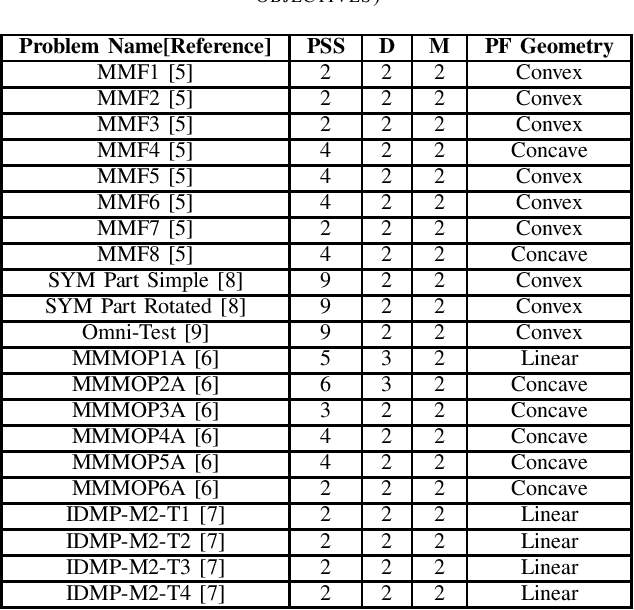
In solving multi-modal, multi-objective optimization problems (MMOPs), the objective is not only to find a good representation of the Pareto-optimal front (PF) in the objective space but also to find all equivalent Pareto-optimal subsets (PSS) in the variable space. Such problems are practically relevant when a decision maker (DM) is interested in identifying alternative designs with similar performance. There has been significant research interest in recent years to develop efficient algorithms to deal with MMOPs. However, the existing algorithms still require prohibitive number of function evaluations (often in several thousands) to deal with problems involving as low as two objectives and two variables. The algorithms are typically embedded with sophisticated, customized mechanisms that require additional parameters to manage the diversity and convergence in the variable and the objective spaces. In this letter, we introduce a steady-state evolutionary algorithm for solving MMOPs, with a simple design and no additional userdefined parameters that need tuning compared to a standard EA. We report its performance on 21 MMOPs from various test suites that are widely used for benchmarking using a low computational budget of 1000 function evaluations. The performance of the proposed algorithm is compared with six state-of-the-art algorithms (MO Ring PSO SCD, DN-NSGAII, TriMOEA-TA&R, CPDEA, MMOEA/DC and MMEA-WI). The proposed algorithm exhibits significantly better performance than the above algorithms based on the established metrics including IGDX, PSP and IGD. We hope this study would encourage design of simple, efficient and generalized algorithms to improve its uptake for practical applications.