Pareto Set Prediction Assisted Bilevel Multi-objective Optimization
Paper and Code
Sep 05, 2024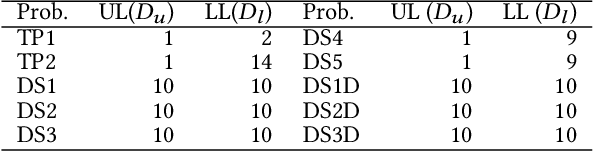
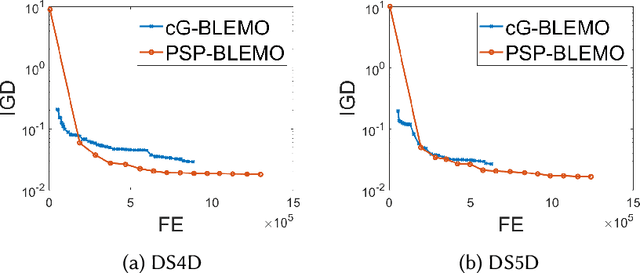
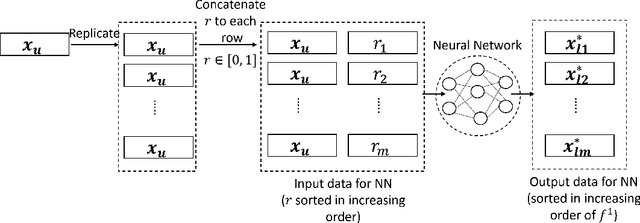

Bilevel optimization problems comprise an upper level optimization task that contains a lower level optimization task as a constraint. While there is a significant and growing literature devoted to solving bilevel problems with single objective at both levels using evolutionary computation, there is relatively scarce work done to address problems with multiple objectives (BLMOP) at both levels. For black-box BLMOPs, the existing evolutionary techniques typically utilize nested search, which in its native form consumes large number of function evaluations. In this work, we propose to reduce this expense by predicting the lower level Pareto set for a candidate upper level solution directly, instead of conducting an optimization from scratch. Such a prediction is significantly challenging for BLMOPs as it involves one-to-many mapping scenario. We resolve this bottleneck by supplementing the dataset using a helper variable and construct a neural network, which can then be trained to map the variables in a meaningful manner. Then, we embed this initialization within a bilevel optimization framework, termed Pareto set prediction assisted evolutionary bilevel multi-objective optimization (PSP-BLEMO). Systematic experiments with existing state-of-the-art methods are presented to demonstrate its benefit. The experiments show that the proposed approach is competitive across a range of problems, including both deceptive and non-deceptive problems
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge