Is Probing All You Need? Indicator Tasks as an Alternative to Probing Embedding Spaces

The ability to identify and control different kinds of linguistic information encoded in vector representations of words has many use cases, especially for explainability and bias removal. This is usually done via a set of simple classification tasks, termed probes, to evaluate the information encoded in the embedding space. However, the involvement of a trainable classifier leads to entanglement between the probe's results and the classifier's nature. As a result, contemporary works on probing include tasks that do not involve training of auxiliary models. In this work we introduce the term indicator tasks for non-trainable tasks which are used to query embedding spaces for the existence of certain properties, and claim that this kind of tasks may point to a direction opposite to probes, and that this contradiction complicates the decision on whether a property exists in an embedding space. We demonstrate our claims with two test cases, one dealing with gender debiasing and another with the erasure of morphological information from embedding spaces. We show that the application of a suitable indicator provides a more accurate picture of the information captured and removed compared to probes. We thus conclude that indicator tasks should be implemented and taken into consideration when eliciting information from embedded representations.

Ranking Recovery from Limited Comparisons using Low-Rank Matrix Completion

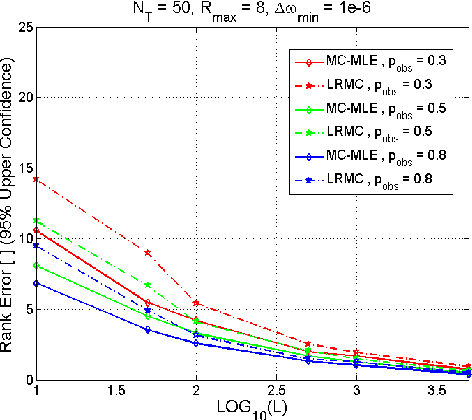
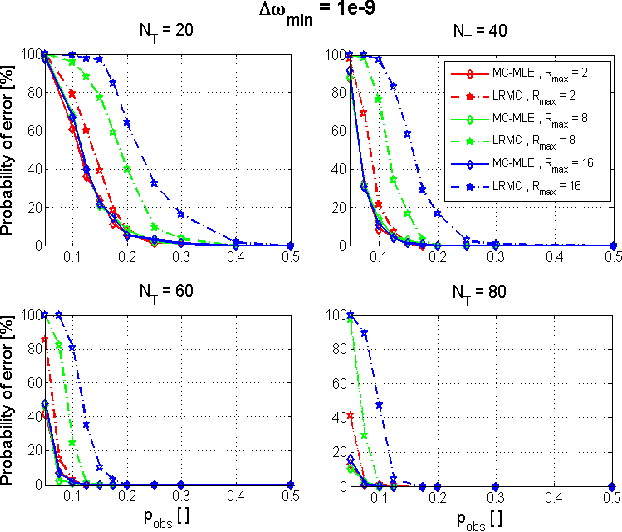
This paper proposes a new method for solving the well-known rank aggregation problem from pairwise comparisons using the method of low-rank matrix completion. The partial and noisy data of pairwise comparisons is transformed into a matrix form. We then use tools from matrix completion, which has served as a major component in the low-rank completion solution of the Netflix challenge, to construct the preference of the different objects. In our approach, the data of multiple comparisons is used to create an estimate of the probability of object i to win (or be chosen) over object j, where only a partial set of comparisons between N objects is known. The data is then transformed into a matrix form for which the noiseless solution has a known rank of one. An alternating minimization algorithm, in which the target matrix takes a bilinear form, is then used in combination with maximum likelihood estimation for both factors. The reconstructed matrix is used to obtain the true underlying preference intensity. This work demonstrates the improvement of our proposed algorithm over the current state-of-the-art in both simulated scenarios and real data.