Ranking Recovery from Limited Comparisons using Low-Rank Matrix Completion
Paper and Code
Jun 14, 2018
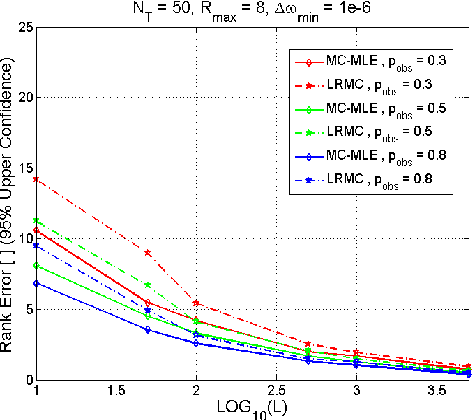
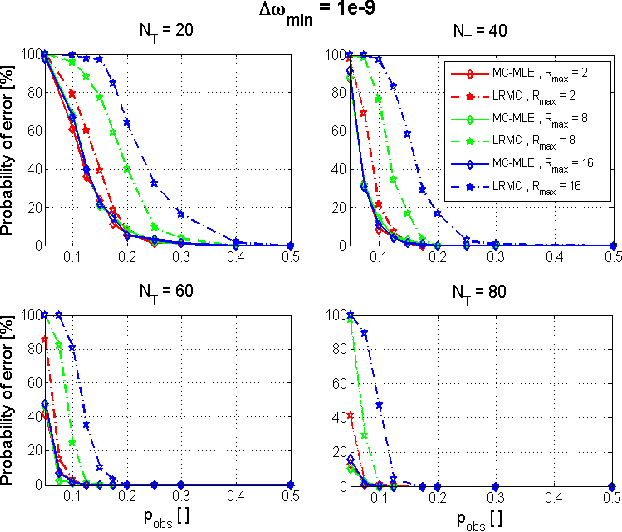

This paper proposes a new method for solving the well-known rank aggregation problem from pairwise comparisons using the method of low-rank matrix completion. The partial and noisy data of pairwise comparisons is transformed into a matrix form. We then use tools from matrix completion, which has served as a major component in the low-rank completion solution of the Netflix challenge, to construct the preference of the different objects. In our approach, the data of multiple comparisons is used to create an estimate of the probability of object i to win (or be chosen) over object j, where only a partial set of comparisons between N objects is known. The data is then transformed into a matrix form for which the noiseless solution has a known rank of one. An alternating minimization algorithm, in which the target matrix takes a bilinear form, is then used in combination with maximum likelihood estimation for both factors. The reconstructed matrix is used to obtain the true underlying preference intensity. This work demonstrates the improvement of our proposed algorithm over the current state-of-the-art in both simulated scenarios and real data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge