Radar-Based Noncontact Measurement of Heartbeat of Humans and Chimpanzees Using Millimeter-Wave Radar with Topology Method

This study proposes a method to determine the filter parameters required for the topology method, which is a radar-based noncontact method for measurement of heart inter-beat intervals. The effectiveness of the proposed method is evaluated by performing radar measurements involving both human participants and chimpanzee subjects. The proposed method is designed to enable setting of the filter cutoff frequency to eliminate respiratory components while maintaining the higher harmonics of the heartbeat components. Measurements using a millimeter-wave radar system and a reference contact-type electrocardiogram sensor demonstrate that the smallest errors that occur when measuring heart inter-beat intervals using the proposed method can be as small as 4.43 and 2.55 ms for humans and chimpanzees, respectively. These results indicate the possibility of using noncontact physiological measurements to monitor both humans and chimpanzees.

Classifying topological sector via machine learning

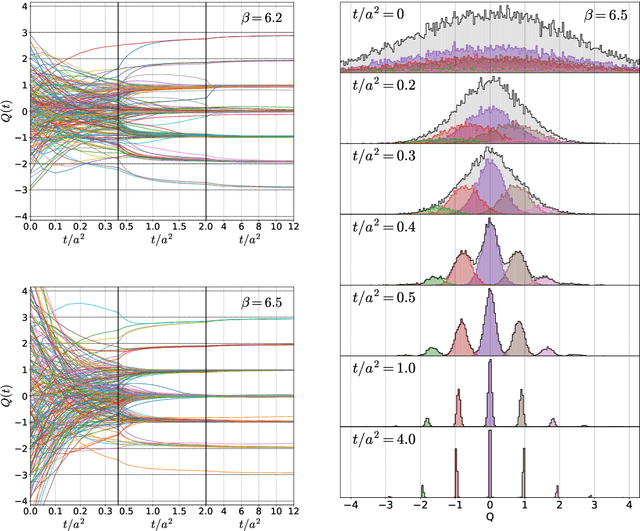
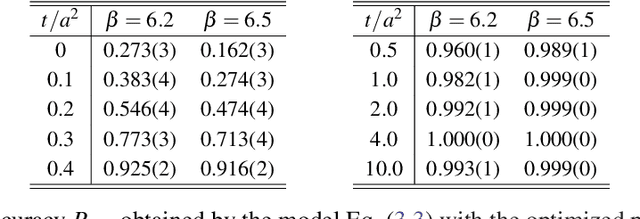
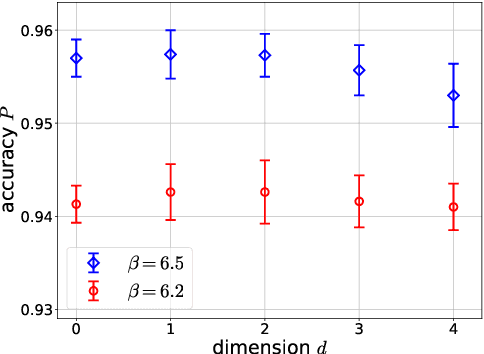
We employ a machine learning technique for an estimate of the topological charge $Q$ of gauge configurations in SU(3) Yang-Mills theory in vacuum. As a first trial, we feed the four-dimensional topological charge density with and without smoothing into the convolutional neural network and train it to estimate the value of $Q$. We find that the trained neural network can estimate the value of $Q$ from the topological charge density at small flow time with high accuracy. Next, we perform the dimensional reduction of the input data as a preprocessing and analyze lower dimensional data by the neural network. We find that the accuracy of the neural network does not have statistically-significant dependence on the dimension of the input data. From this result we argue that the neural network does not find characteristic features responsible for the determination of $Q$ in the higher dimensional space.

Classifying Topological Charge in SU(3) Yang-Mills Theory with Machine Learning

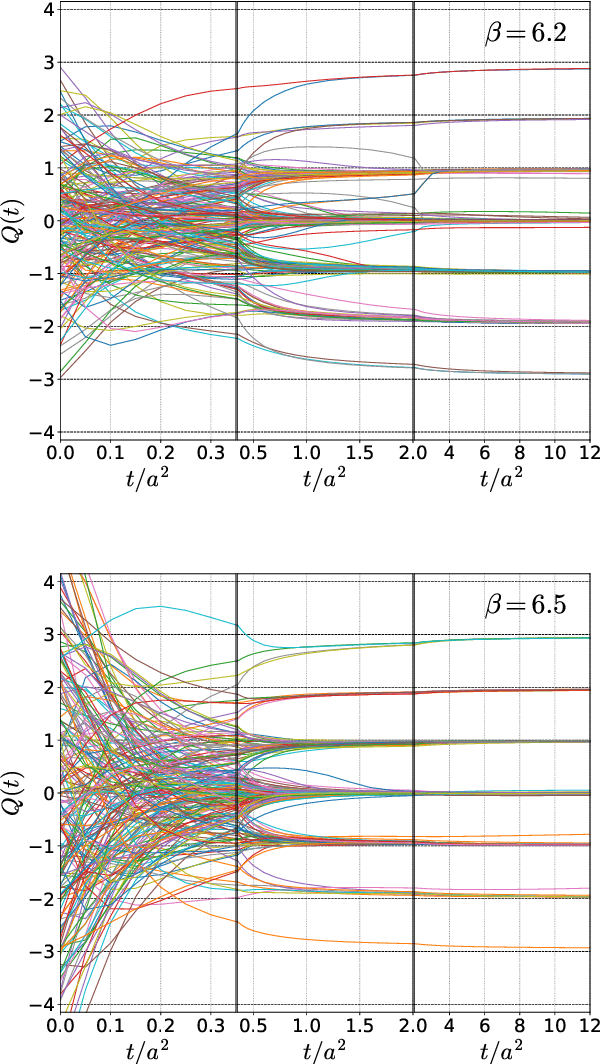
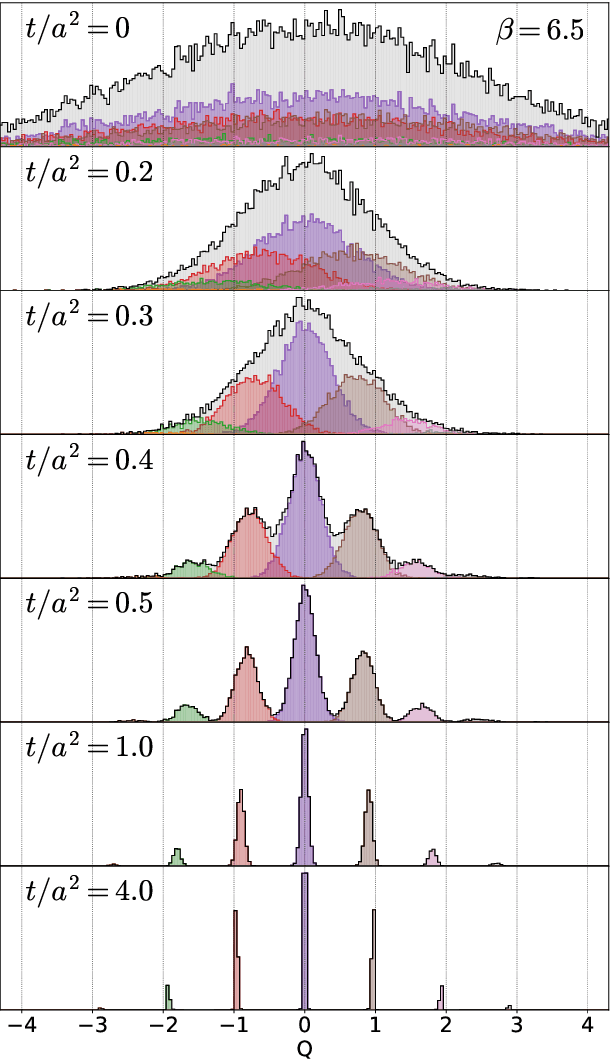
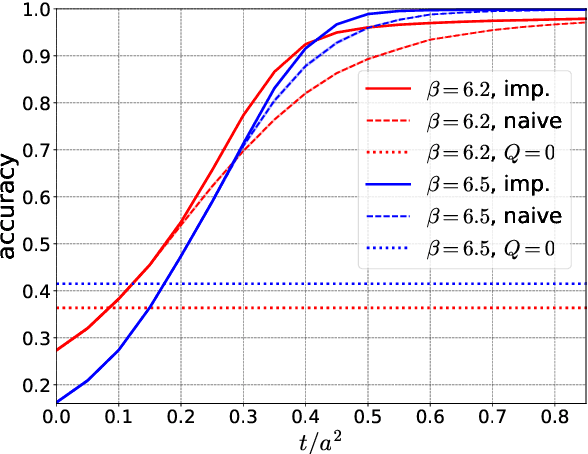
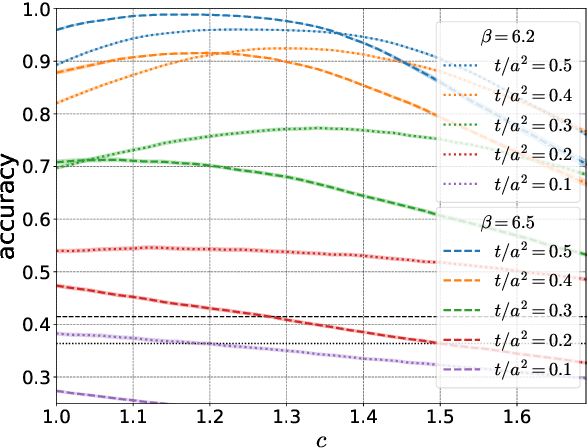
We apply a machine learning technique for identifying the topological charge of quantum gauge configurations in four-dimensional SU(3) Yang-Mills theory. The topological charge density measured on the original and smoothed gauge configurations with and without dimensional reduction is used for inputs of the neural networks (NN) with and without convolutional layers. The gradient flow is used for the smoothing of the gauge field. We find that the topological charge determined at a large flow time can be predicted with high accuracy from the data at small flow times by the trained NN; the accuracy exceeds $99\%$ with the data at $t/a^2\le0.3$. High robustness against the change of simulation parameters is also confirmed. We find that the best performance is obtained when the spatial coordinates of the topological charge density are fully integrated out as a preprocessing, which implies that our convolutional NN does not find characteristic structures in multi-dimensional space relevant for the determination of the topological charge.