Classifying Topological Charge in SU(3) Yang-Mills Theory with Machine Learning

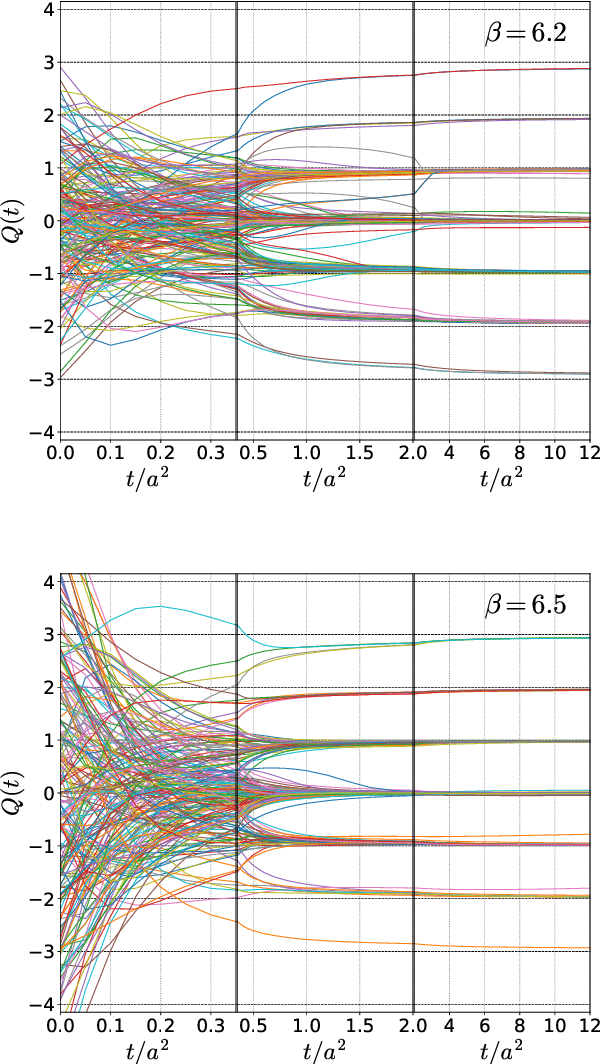
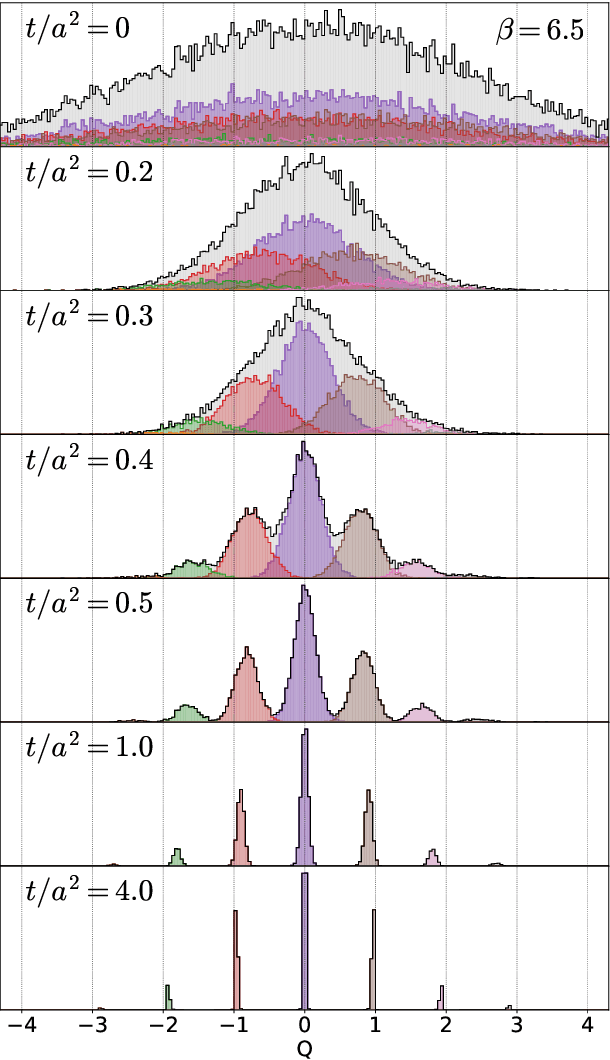
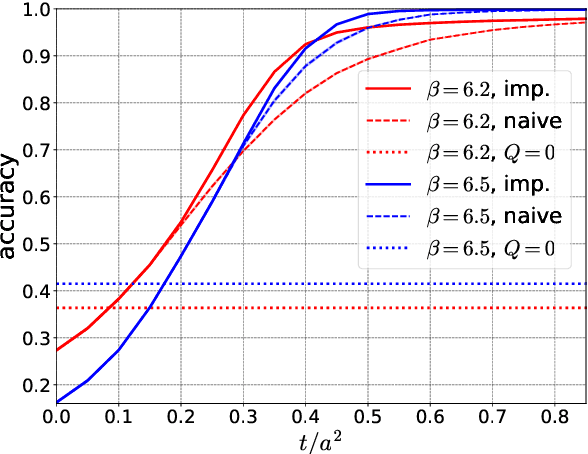
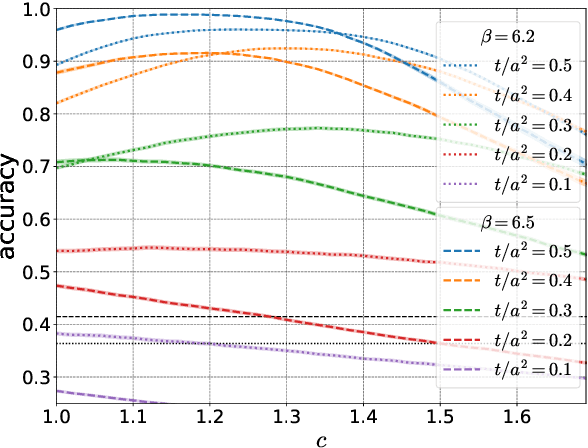
We apply a machine learning technique for identifying the topological charge of quantum gauge configurations in four-dimensional SU(3) Yang-Mills theory. The topological charge density measured on the original and smoothed gauge configurations with and without dimensional reduction is used for inputs of the neural networks (NN) with and without convolutional layers. The gradient flow is used for the smoothing of the gauge field. We find that the topological charge determined at a large flow time can be predicted with high accuracy from the data at small flow times by the trained NN; the accuracy exceeds $99\%$ with the data at $t/a^2\le0.3$. High robustness against the change of simulation parameters is also confirmed. We find that the best performance is obtained when the spatial coordinates of the topological charge density are fully integrated out as a preprocessing, which implies that our convolutional NN does not find characteristic structures in multi-dimensional space relevant for the determination of the topological charge.