Learning Weighted Finite Automata over the Max-Plus Semiring and its Termination

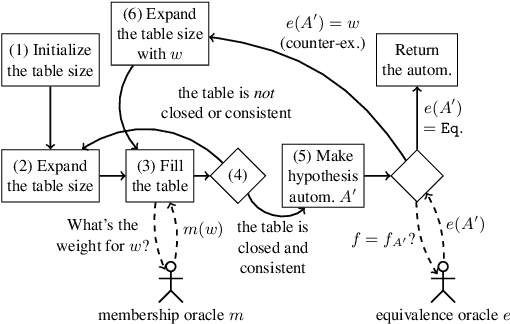
Active learning of finite automata has been vigorously pursued for the purposes of analysis and explanation of black-box systems. In this paper, we study an L*-style learning algorithm for weighted automata over the max-plus semiring. The max-plus setting exposes a "consistency" issue in the previously studied semiring-generic extension of L*: we show that it can fail to maintain consistency of tables, and can thus make equivalence queries on obviously wrong hypothesis automata. We present a theoretical fix by a mathematically clean notion of column-closedness. We also present a nontrivial and reasonably broad class of weighted languages over the max-plus semiring in which our algorithm terminates.

Genetic Algorithm for the Weight Maximization Problem on Weighted Automata

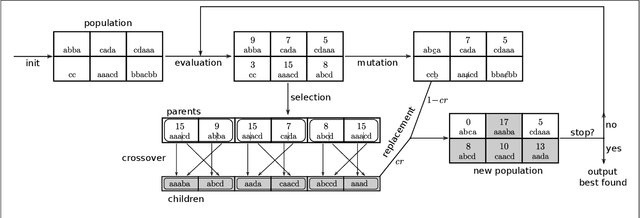
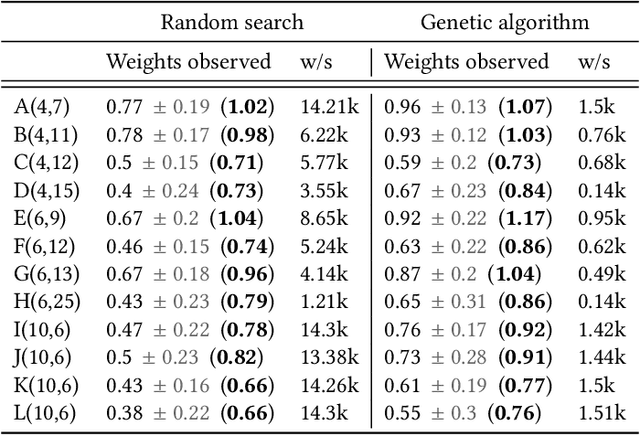
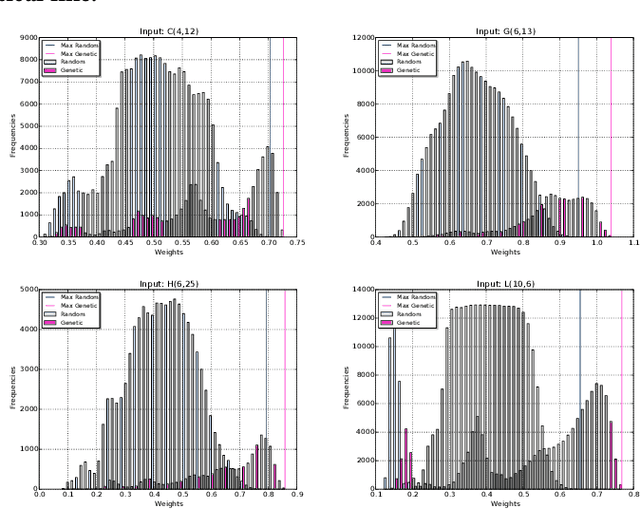
The weight maximization problem (WMP) is the problem of finding the word of highest weight on a weighted finite state automaton (WFA). It is an essential question that emerges in many optimization problems in automata theory. Unfortunately, the general problem can be shown to be undecidable, whereas its bounded decisional version is NP-complete. Designing efficient algorithms that produce approximate solutions to the WMP in reasonable time is an appealing research direction that can lead to several new applications including formal verification of systems abstracted as WFAs. In particular, in combination with a recent procedure that translates a recurrent neural network into a weighted automaton, an algorithm for the WMP can be used to analyze and verify the network by exploiting the simpler and more compact automata model. In this work, we propose, implement and evaluate a metaheuristic based on genetic algorithms to approximate solutions to the WMP. We experimentally evaluate its performance on examples from the literature and show its potential on different applications.

Weighted Automata Extraction from Recurrent Neural Networks via Regression on State Spaces

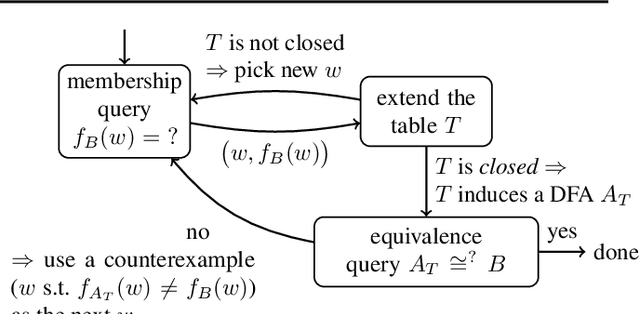
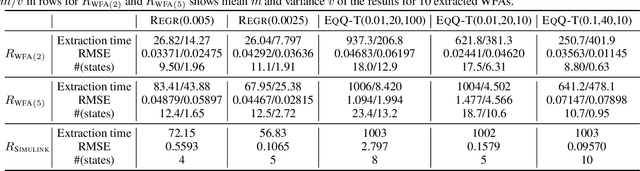
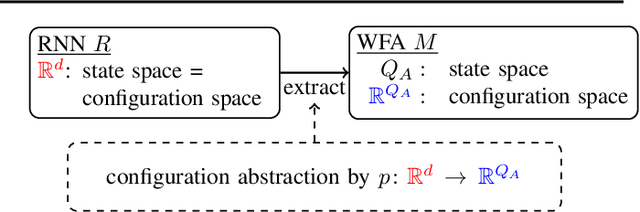
We present a method to extract a weighted finite automaton (WFA) from a recurrent neural network (RNN). Our algorithm is based on the WFA learning algorithm by Balle and Mohri, which is in turn an extension of Angluin's classic \lstar algorithm. Our technical novelty is in the use of \emph{regression} methods for the so-called equivalence queries, thus exploiting the internal state space of an RNN. This way we achieve a quantitative extension of the recent work by Weiss, Goldberg and Yahav that extracts DFAs. Experiments demonstrate that our algorithm's practicality.