Genetic Algorithm for the Weight Maximization Problem on Weighted Automata
Paper and Code
Apr 11, 2020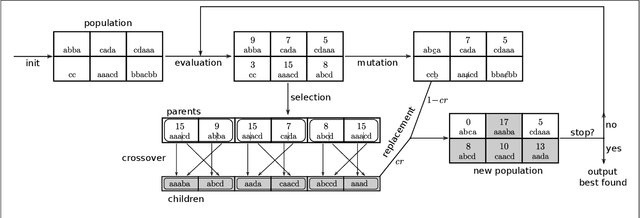

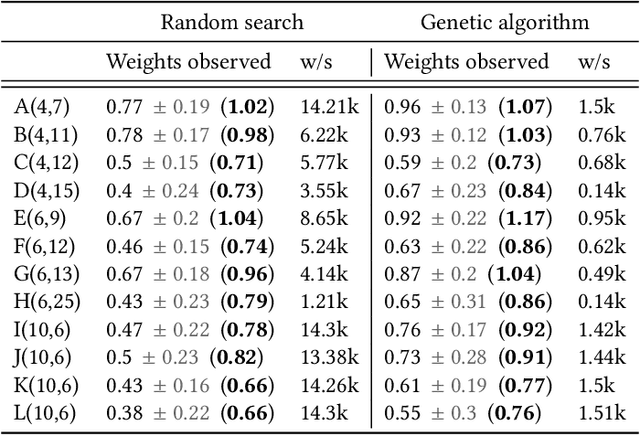
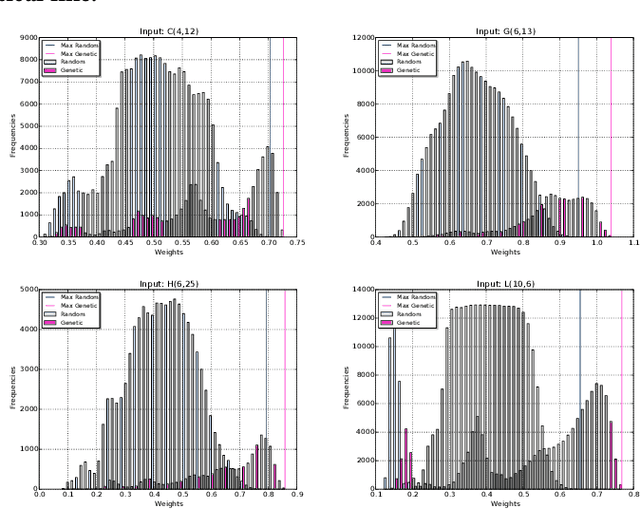
The weight maximization problem (WMP) is the problem of finding the word of highest weight on a weighted finite state automaton (WFA). It is an essential question that emerges in many optimization problems in automata theory. Unfortunately, the general problem can be shown to be undecidable, whereas its bounded decisional version is NP-complete. Designing efficient algorithms that produce approximate solutions to the WMP in reasonable time is an appealing research direction that can lead to several new applications including formal verification of systems abstracted as WFAs. In particular, in combination with a recent procedure that translates a recurrent neural network into a weighted automaton, an algorithm for the WMP can be used to analyze and verify the network by exploiting the simpler and more compact automata model. In this work, we propose, implement and evaluate a metaheuristic based on genetic algorithms to approximate solutions to the WMP. We experimentally evaluate its performance on examples from the literature and show its potential on different applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge