Stability and Robustness of the Disturbance Observer-based Motion Control Systems in Discrete-Time Domain

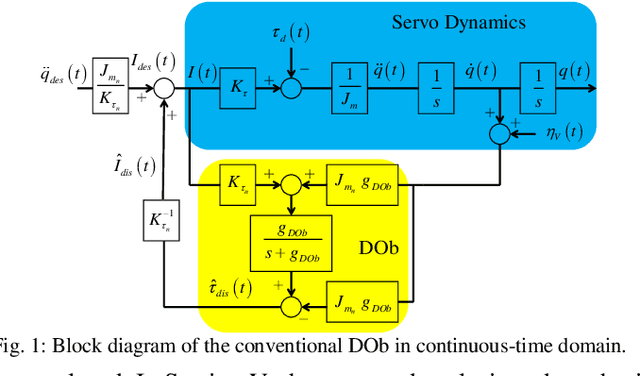
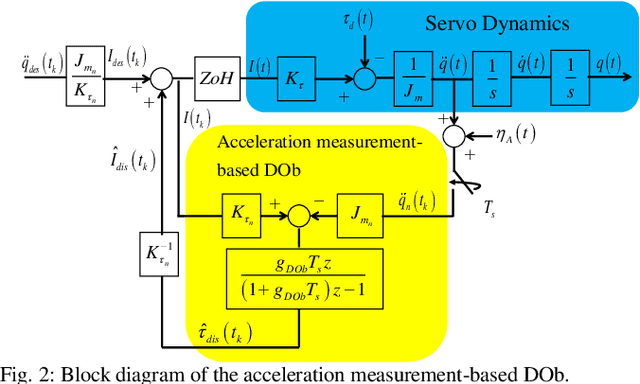
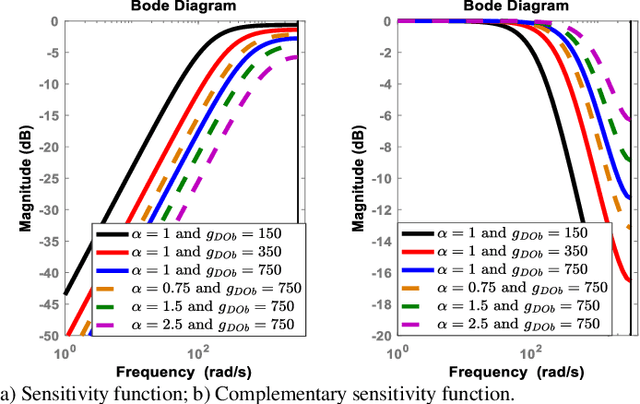
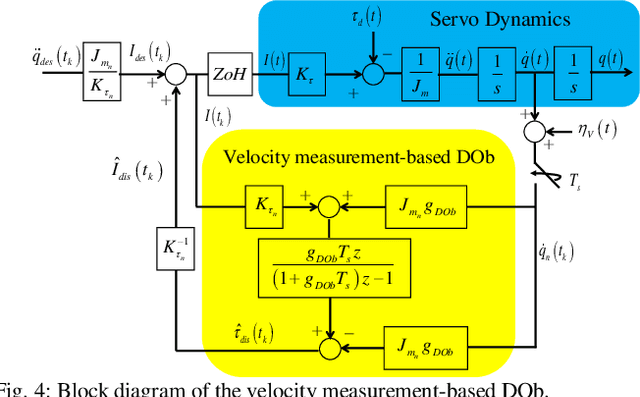
This paper analyses the robust stability and performance of the Disturbance Observer- (DOb-) based digital motion control systems in discrete-time domain. It is shown that the phase margin and the robustness of the digital motion controller can be directly adjusted by tuning the nominal plant model and the bandwidth of the observer. However, they have upper and lower bounds due to robust stability and performance constraints as well as noise-sensitivity. The constraints on the design parameters of the DOb change when the digital motion controller is synthesised by measuring different states of a servo system. For example, the bandwidth of the DOb is limited by noise-sensitivity and waterbed effect when velocity and position measurements are employed in the digital robust motion controller synthesis. The robustness constraint due to the waterbed effect is removed when the DOb is implemented by acceleration measurement. The design constraints on the nominal plant model and the bandwidth of the observer are analytically derived by employing the generalised Bode Integral Theorem in discrete-time. The proposed design constraints allow one to systematically synthesise a high-performance DOb-based digital robust motion controller. Experimental results are given to verify the proposed analysis and synthesis methods.

A Stability Analysis for the Acceleration-based Robust Position Control of Robot Manipulators via Disturbance Observer

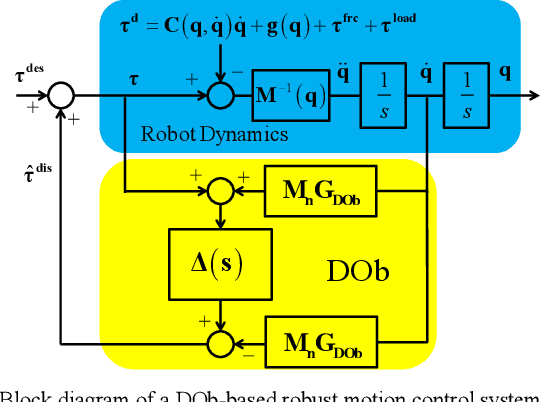
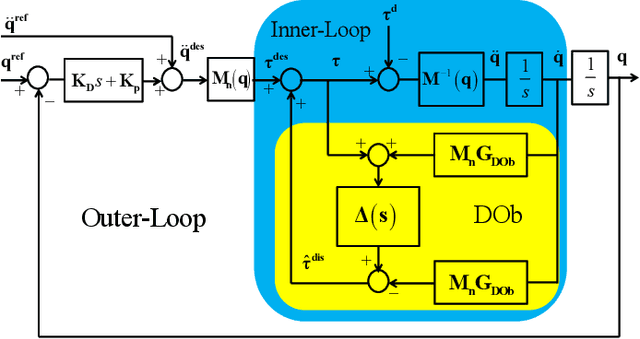
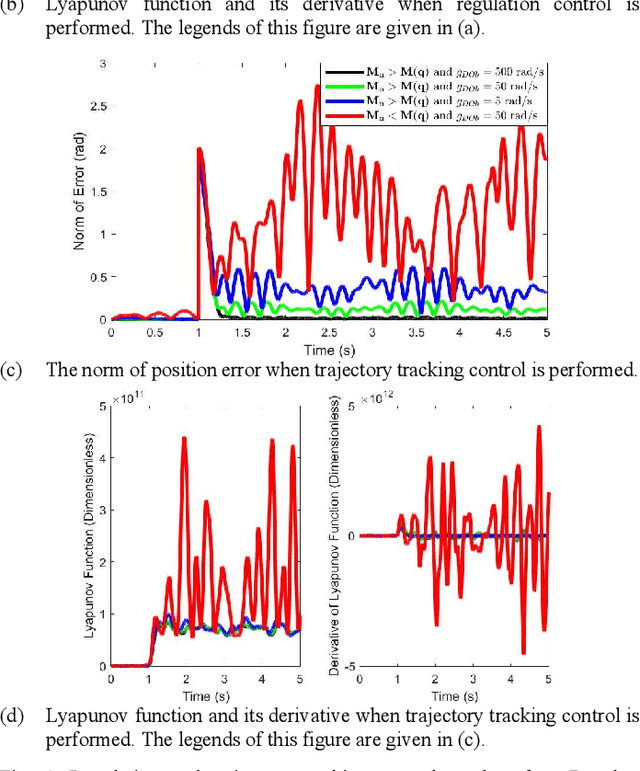
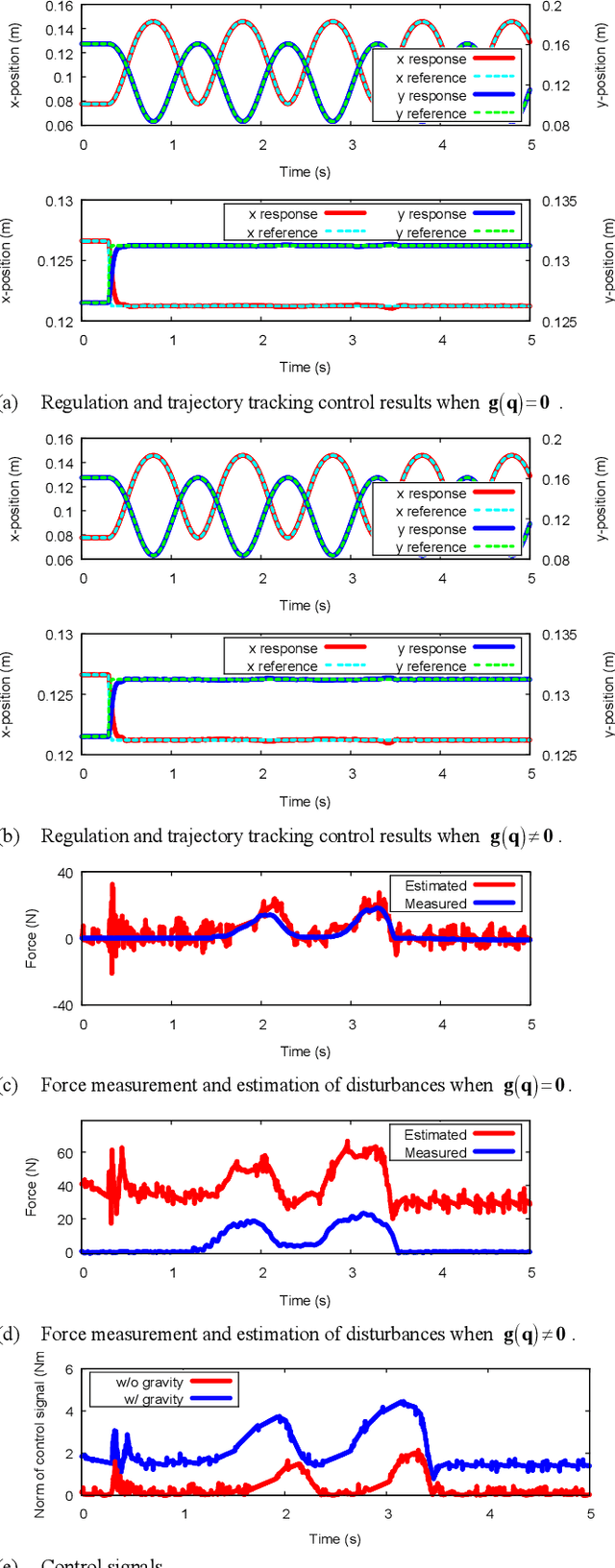
This paper proposes a new nonlinear stability analysis for the acceleration-based robust position control of robot manipulators by using Disturbance Observer (DOb). It is shown that if the nominal inertia matrix is properly tuned in the design of DOb, then the position error asymptotically goes to zero in regulation control and is uniformly ultimately bounded in trajectory tracking control. As the bandwidth of DOb and the nominal inertia matrix are increased, the bound of error shrinks, i.e., the robust stability and performance of the position control system are improved. However, neither the bandwidth of DOb nor the nominal inertia matrix can be freely increased due to practical design constraints, e.g., the robust position controller becomes more noise sensitive when they are increased. The proposed stability analysis provides insights regarding the dynamic behavior of DOb-based robust motion control systems. It is theoretically and experimentally proved that non-diagonal elements of the nominal inertia matrix are useful to improve the stability and adjust the trade-off between the robustness and noise sensitivity. The validity of the proposal is verified by simulation and experimental results.