Orthogonal Series Estimation for the Ratio of Conditional Expectation Functions

In various fields of data science, researchers are often interested in estimating the ratio of conditional expectation functions (CEFR). Specifically in causal inference problems, it is sometimes natural to consider ratio-based treatment effects, such as odds ratios and hazard ratios, and even difference-based treatment effects are identified as CEFR in some empirically relevant settings. This chapter develops the general framework for estimation and inference on CEFR, which allows the use of flexible machine learning for infinite-dimensional nuisance parameters. In the first stage of the framework, the orthogonal signals are constructed using debiased machine learning techniques to mitigate the negative impacts of the regularization bias in the nuisance estimates on the target estimates. The signals are then combined with a novel series estimator tailored for CEFR. We derive the pointwise and uniform asymptotic results for estimation and inference on CEFR, including the validity of the Gaussian bootstrap, and provide low-level sufficient conditions to apply the proposed framework to some specific examples. We demonstrate the finite-sample performance of the series estimator constructed under the proposed framework by numerical simulations. Finally, we apply the proposed method to estimate the causal effect of the 401(k) program on household assets.

Estimation of Local Average Treatment Effect by Data Combination

It is important to estimate the local average treatment effect (LATE) when compliance with a treatment assignment is incomplete. The previously proposed methods for LATE estimation required all relevant variables to be jointly observed in a single dataset; however, it is sometimes difficult or even impossible to collect such data in many real-world problems for technical or privacy reasons. We consider a novel problem setting in which LATE, as a function of covariates, is nonparametrically identified from the combination of separately observed datasets. For estimation, we show that the direct least squares method, which was originally developed for estimating the average treatment effect under complete compliance, is applicable to our setting. However, model selection and hyperparameter tuning for the direct least squares estimator can be unstable in practice since it is defined as a solution to the minimax problem. We then propose a weighted least squares estimator that enables simpler model selection by avoiding the minimax objective formulation. Unlike the inverse probability weighted (IPW) estimator, the proposed estimator directly uses the pre-estimated weight without inversion, avoiding the problems caused by the IPW methods. We demonstrate the effectiveness of our method through experiments using synthetic and real-world datasets.

Bayesian data combination model with Gaussian process latent variable model for mixed observed variables under NMAR missingness

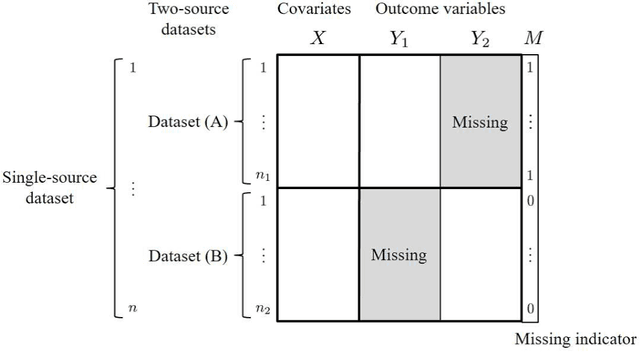
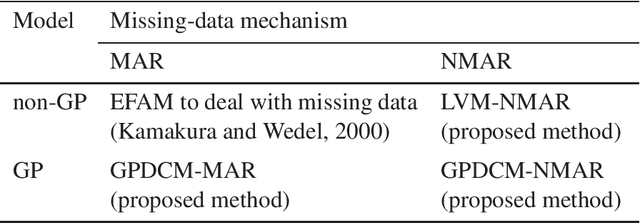
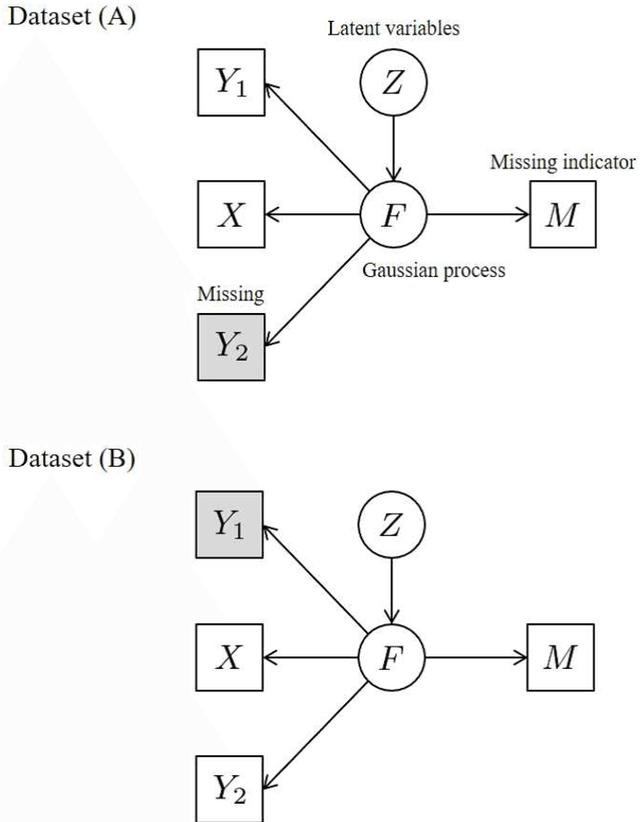
In the analysis of observational data in social sciences and businesses, it is difficult to obtain a "(quasi) single-source dataset" in which the variables of interest are simultaneously observed. Instead, multiple-source datasets are typically acquired for different individuals or units. Various methods have been proposed to investigate the relationship between the variables in each dataset, e.g., matching and latent variable modeling. It is necessary to utilize these datasets as a single-source dataset with missing variables. Existing methods assume that the datasets to be integrated are acquired from the same population or that the sampling depends on covariates. This assumption is referred to as missing at random (MAR) in terms of missingness. However, as will been shown in application studies, it is likely that this assumption does not hold in actual data analysis and the results obtained may be biased. We propose a data fusion method that does not assume that datasets are homogenous. We use a Gaussian process latent variable model for non-MAR missing data. This model assumes that the variables of concern and the probability of being missing depend on latent variables. A simulation study and real-world data analysis show that the proposed method with a missing-data mechanism and the latent Gaussian process yields valid estimates, whereas an existing method provides severely biased estimates. This is the first study in which non-random assignment to datasets is considered and resolved under resonable assumptions in data fusion problem.

Positive-Unlabelled Survival Data Analysis

In this paper, we consider a novel framework of positive-unlabeled data in which as positive data survival times are observed for subjects who have events during the observation time as positive data and as unlabeled data censoring times are observed but whether the event occurs or not are unknown for some subjects. We consider two cases: (1) when censoring time is observed in positive data, and (2) when it is not observed. For both cases, we developed parametric models, nonparametric models, and machine learning models and the estimation strategies for these models. Simulation studies show that under this data setup, traditional survival analysis may yield severely biased results, while the proposed estimation method can provide valid results.

A Contextual Bandit Algorithm for Ad Creative under Ad Fatigue

Selecting ad creative is one of the most important task for DSPs (Demand-Side Platform) in online advertising. DSPs should not only consider the effectiveness of the ad creative but also the user's psychological status when selecting ad creative. In this study, we propose an efficient and easy-to-implement ad creative selection algorithm that explicitly considers wear-in and wear-out effects of ad creative due to the repetitive ad exposures. The proposed system was deployed in a real-world production environment and tested against the baseline. It out-performed the existing system in most of the KPIs.