Bayesian data combination model with Gaussian process latent variable model for mixed observed variables under NMAR missingness
Paper and Code
Sep 01, 2021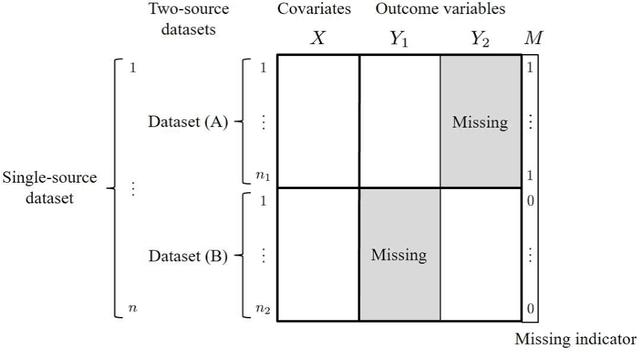
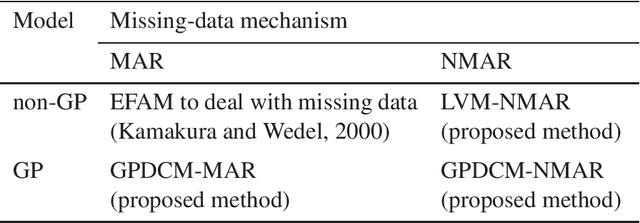
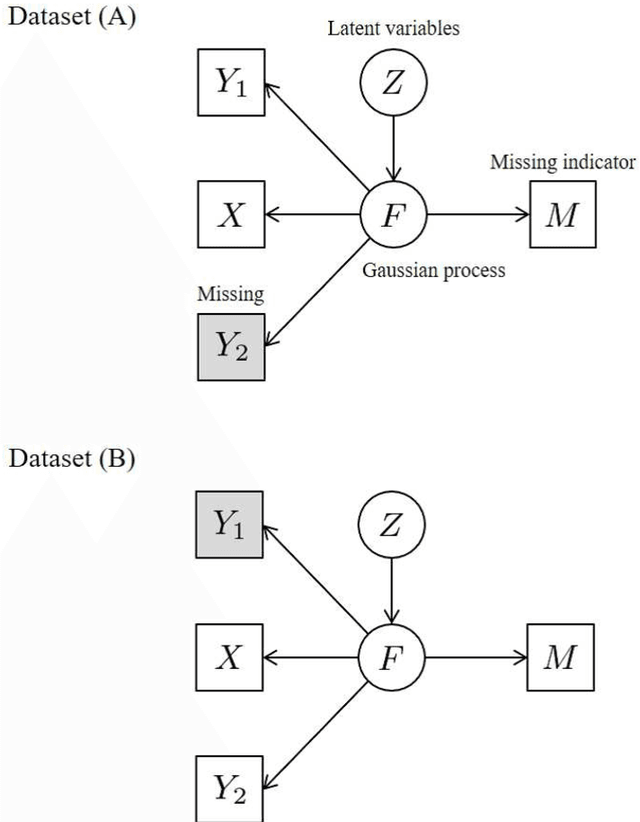
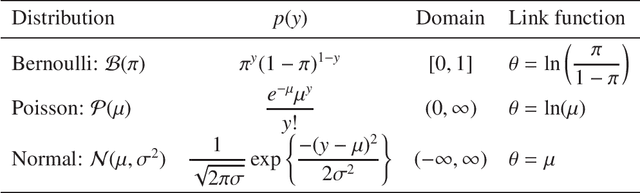
In the analysis of observational data in social sciences and businesses, it is difficult to obtain a "(quasi) single-source dataset" in which the variables of interest are simultaneously observed. Instead, multiple-source datasets are typically acquired for different individuals or units. Various methods have been proposed to investigate the relationship between the variables in each dataset, e.g., matching and latent variable modeling. It is necessary to utilize these datasets as a single-source dataset with missing variables. Existing methods assume that the datasets to be integrated are acquired from the same population or that the sampling depends on covariates. This assumption is referred to as missing at random (MAR) in terms of missingness. However, as will been shown in application studies, it is likely that this assumption does not hold in actual data analysis and the results obtained may be biased. We propose a data fusion method that does not assume that datasets are homogenous. We use a Gaussian process latent variable model for non-MAR missing data. This model assumes that the variables of concern and the probability of being missing depend on latent variables. A simulation study and real-world data analysis show that the proposed method with a missing-data mechanism and the latent Gaussian process yields valid estimates, whereas an existing method provides severely biased estimates. This is the first study in which non-random assignment to datasets is considered and resolved under resonable assumptions in data fusion problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge