3D/2D Registration of Angiograms using Silhouette-based Differentiable Rendering

We present a method for 3D/2D registration of Digital Subtraction Angiography (DSA) images to provide valuable insight into brain hemodynamics and angioarchitecture. Our approach formulates the registration as a pose estimation problem, leveraging both anteroposterior and lateral DSA views and employing differentiable rendering. Preliminary experiments on real and synthetic datasets demonstrate the effectiveness of our method, with both qualitative and quantitative evaluations highlighting its potential for clinical applications. The code is available at https://github.com/taewoonglee17/TwoViewsDSAReg.

Fluctuation-dissipation Type Theorem in Stochastic Linear Learning

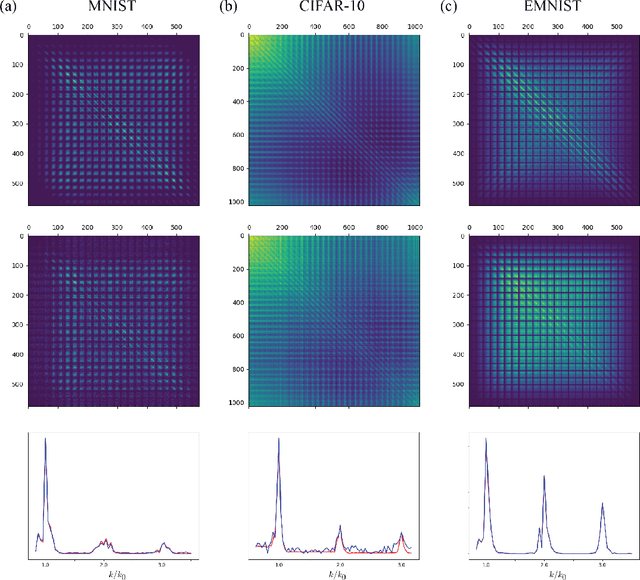
The fluctuation-dissipation theorem (FDT) is a simple yet powerful consequence of the first-order differential equation governing the dynamics of systems subject simultaneously to dissipative and stochastic forces. The linear learning dynamics, in which the input vector maps to the output vector by a linear matrix whose elements are the subject of learning, has a stochastic version closely mimicking the Langevin dynamics when a full-batch gradient descent scheme is replaced by that of stochastic gradient descent. We derive a generalized FDT for the stochastic linear learning dynamics and verify its validity among the well-known machine learning data sets such as MNIST, CIFAR-10 and EMNIST.