DDIM Redux: Mathematical Foundation and Some Extension

This note provides a critical review of the mathematical concepts underlying the generalized diffusion denoising implicit model (gDDIM) and the exponential integrator (EI) scheme. We present enhanced mathematical results, including an exact expression for the reverse trajectory in the probability flow ODE and an exact expression for the covariance matrix in the gDDIM scheme. Furthermore, we offer an improved understanding of the EI scheme's efficiency in terms of the change of variables. The noising process in DDIM is analyzed from the perspective of non-equilibrium statistical physics. Additionally, we propose a new scheme for DDIM, called the principal-axis DDIM (paDDIM).

Fluctuation-dissipation Type Theorem in Stochastic Linear Learning

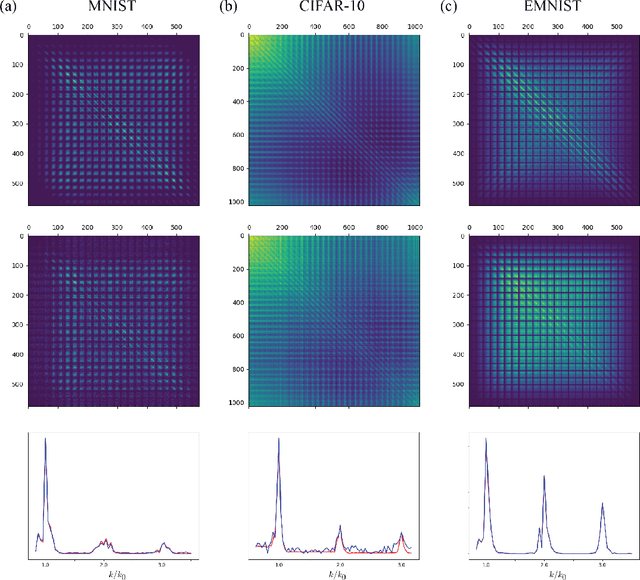
The fluctuation-dissipation theorem (FDT) is a simple yet powerful consequence of the first-order differential equation governing the dynamics of systems subject simultaneously to dissipative and stochastic forces. The linear learning dynamics, in which the input vector maps to the output vector by a linear matrix whose elements are the subject of learning, has a stochastic version closely mimicking the Langevin dynamics when a full-batch gradient descent scheme is replaced by that of stochastic gradient descent. We derive a generalized FDT for the stochastic linear learning dynamics and verify its validity among the well-known machine learning data sets such as MNIST, CIFAR-10 and EMNIST.