Ordinary Differential Equation-based MIMO Signal Detection

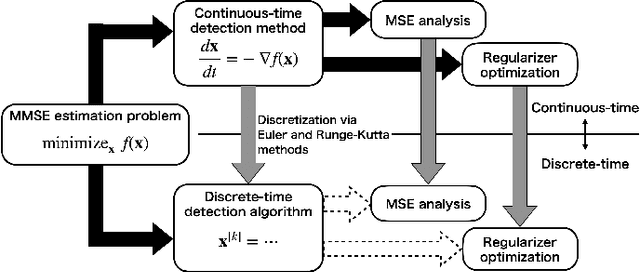
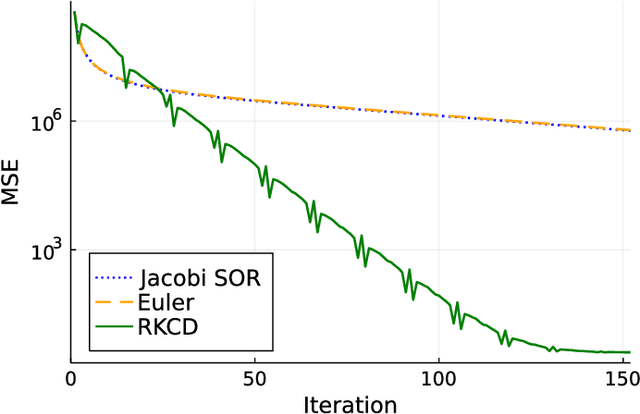
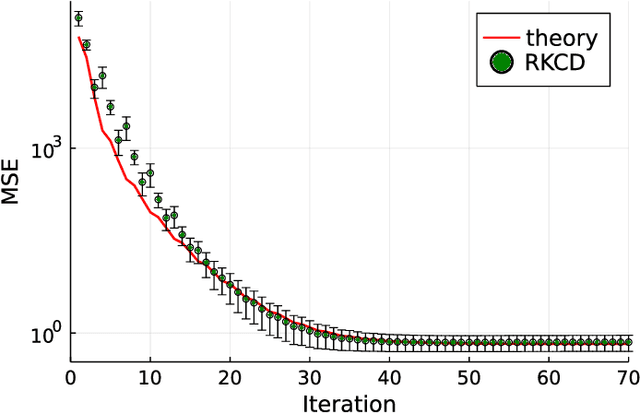
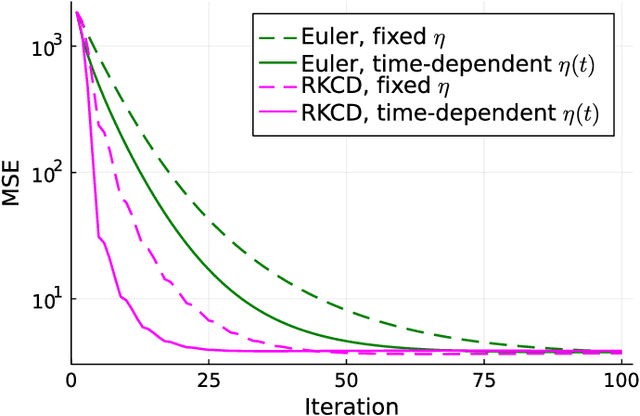
Inspired by the emerging technologies for energy-efficient analog computing and continuous-time processing, this paper proposes a continuous-time minimum mean squared error (MMSE) estimation for multiple-input multiple-output (MIMO) systems based on an ordinary differential equation (ODE). We derive an analytical formula for the mean squared error (MSE) at any given time, which is a primary performance measure for estimation methods in MIMO systems. The MSE of the proposed method depends on the regularization parameter, which affects the convergence properties. In addition, this method is extended by incorporating a time-dependent regularization parameter to enhance convergence performance. Numerical experiments demonstrate excellent consistency with theoretical values and improved convergence performance due to the integration of the time-dependent parameter. Other benefits of the ODE are also discussed in this paper. Discretizing the ODE for MMSE estimation using numerical methods provides insights into the construction and understanding of discrete-time estimation algorithms. We present discrete-time estimation algorithms based on the Euler and Runge-Kutta methods. The performance of the algorithms can be analyzed using the MSE formula for continuous-time methods, and their performance can be improved by using theoretical results in a continuous-time domain. These benefits can only be obtained through formulations using ODE.

Deep Unfolding-based Weighted Averaging for Federated Learning under Heterogeneous Environments

Federated learning is a collaborative model training method by iterating model updates at multiple clients and aggregation of the updates at a central server. Device and statistical heterogeneity of the participating clients cause performance degradation so that an appropriate weight should be assigned per client in the server's aggregation phase. This paper employs deep unfolding to learn the weights that adapt to the heterogeneity, which gives the model with high accuracy on uniform test data. The results of numerical experiments indicate the high performance of the proposed method and the interpretable behavior of the learned weights.

Energy Efficient Over-the-Air Computation for Correlated Data in Wireless Sensor Networks

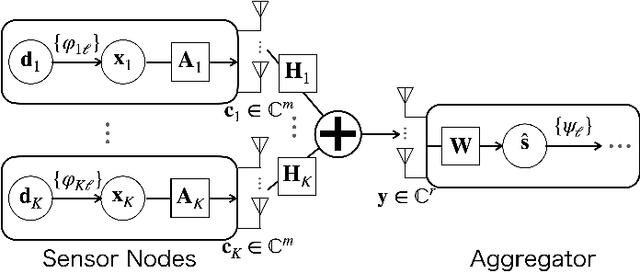
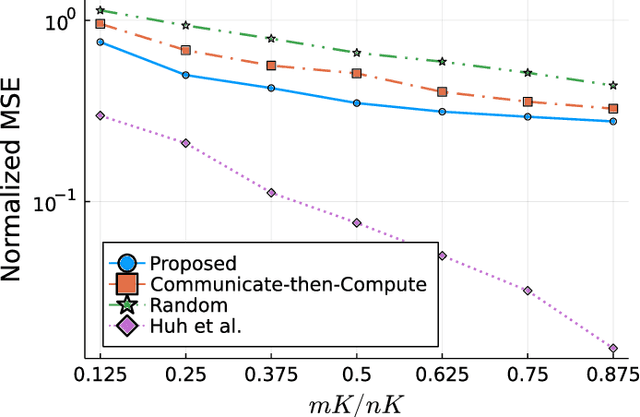
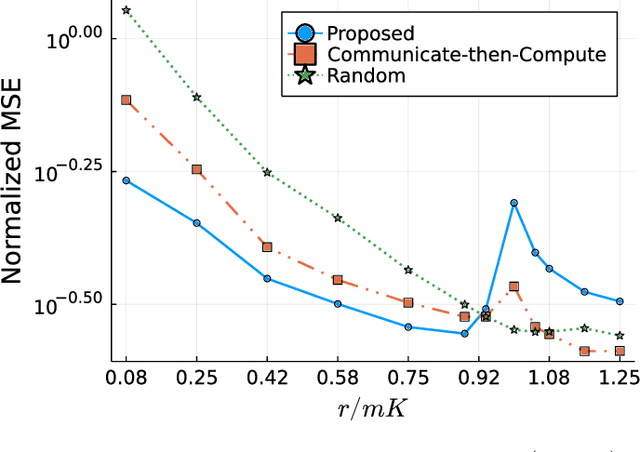
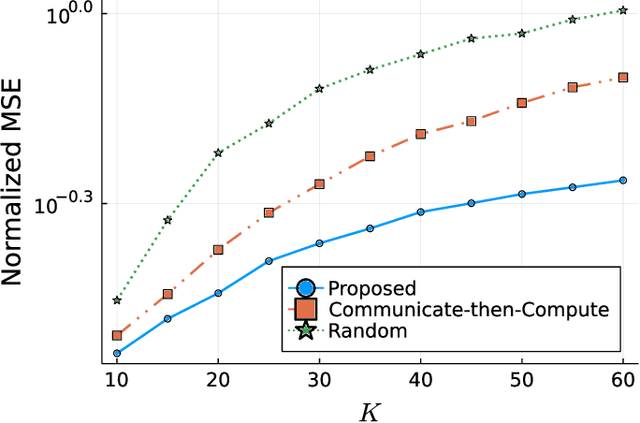
Over-the-air computation (AirComp) enables efficient wireless data aggregation in sensor networks by simultaneous processing of calculation and communication. This paper proposes a novel precoding method for AirComp that incorporates statistical properties of sensing data, spatial correlation and heterogeneous data correlation. The design of the proposed precoding matrix requires no iterative processes so that it can be realized with low computational costs. Moreover, this method provides dimensionality reduction of sensing data to reduce communication costs per sensor. We evaluate performance of the proposed method in terms of various system parameters. The results show the superiority of the proposed method to conventional non-iterative methods in cases where the number of receive antennas at the aggregator is less than that of the total transmit antennas at the sensors.

MMSE Signal Detection for MIMO Systems based on Ordinary Differential Equation

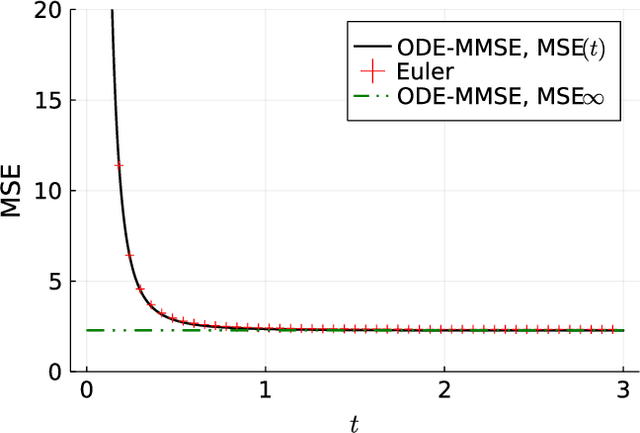
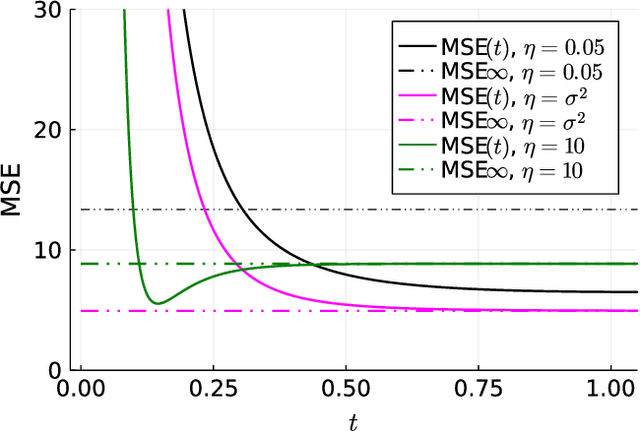
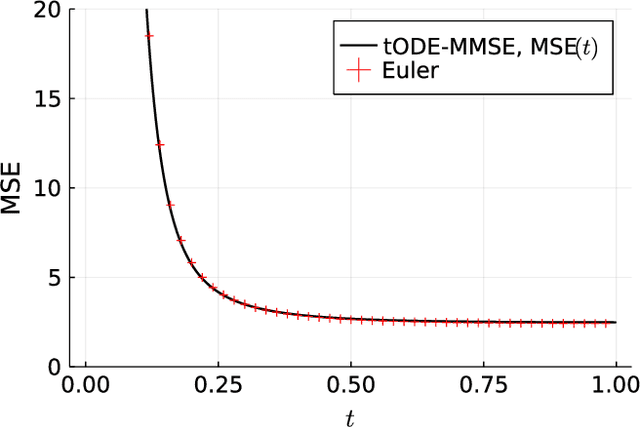
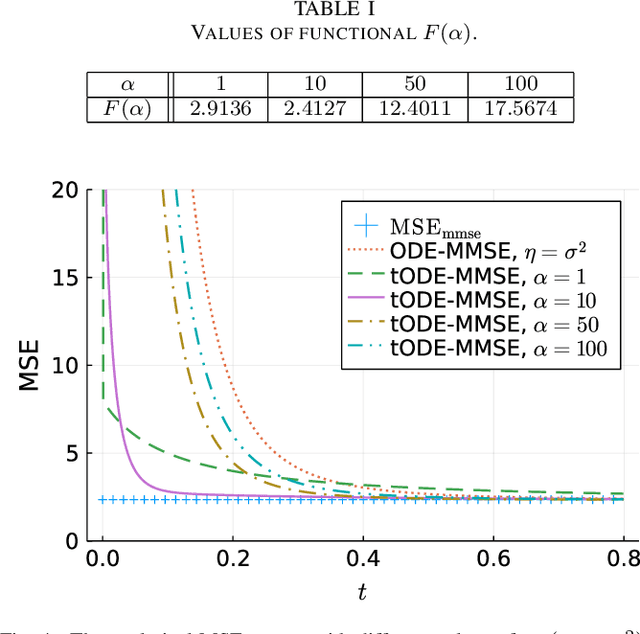
Motivated by emerging technologies for energy efficient analog computing and continuous-time processing, this paper proposes continuous-time minimum mean squared error estimation for multiple-input multiple-output (MIMO) systems based on an ordinary differential equation. Mean squared error (MSE) is a principal detection performance measure of estimation methods for MIMO systems. We derive an analytical MSE formula that indicates the MSE at any time. The MSE of the proposed method depends on a regularization parameter which affects the convergence property of the MSE. Furthermore, we extend the proposed method by using a time-dependent regularization parameter to achieve better convergence performance. Numerical experiments indicated excellent agreement with the theoretical values and improvement in the convergence performance owing to the use of the time-dependent parameter.

Convergence Acceleration via Chebyshev Step: Plausible Interpretation of Deep-Unfolded Gradient Descent

Deep unfolding is a promising deep-learning technique, whose network architecture is based on expanding the recursive structure of existing iterative algorithms. Although convergence acceleration is a remarkable advantage of deep unfolding, its theoretical aspects have not been revealed yet. The first half of this study details the theoretical analysis of the convergence acceleration in deep-unfolded gradient descent (DUGD) whose trainable parameters are step sizes. We propose a plausible interpretation of the learned step-size parameters in DUGD by introducing the principle of Chebyshev steps derived from Chebyshev polynomials. The use of Chebyshev steps in gradient descent (GD) enables us to bound the spectral radius of a matrix governing the convergence speed of GD, leading to a tight upper bound on the convergence rate. The convergence rate of GD using Chebyshev steps is shown to be asymptotically optimal, although it has no momentum terms. We also show that Chebyshev steps numerically explain the learned step-size parameters in DUGD well. In the second half of the study, %we apply the theory of Chebyshev steps and Chebyshev-periodical successive over-relaxation (Chebyshev-PSOR) is proposed for accelerating linear/nonlinear fixed-point iterations. Theoretical analysis and numerical experiments indicate that Chebyshev-PSOR exhibits significantly faster convergence for various examples such as Jacobi method and proximal gradient methods.

Deep Unfolded Multicast Beamforming

Multicast beamforming is a promising technique for multicast communication. Providing an efficient and powerful beamforming design algorithm is a crucial issue because multicast beamforming problems such as a max-min-fair problem are NP-hard in general. Recently, deep learning-based approaches have been proposed for beamforming design. Although these approaches using deep neural networks exhibit reasonable performance gain compared with conventional optimization-based algorithms, their scalability is an emerging problem for large systems in which beamforming design becomes a more demanding task. In this paper, we propose a novel deep unfolded trainable beamforming design with high scalability and efficiency. The algorithm is designed by expanding the recursive structure of an existing algorithm based on projections onto convex sets and embedding a constant number of trainable parameters to the expanded network, which leads to a scalable and stable training process. Numerical results show that the proposed algorithm can accelerate its convergence speed by using unsupervised learning, which is a challenging training process for deep unfolding.

Theoretical Interpretation of Learned Step Size in Deep-Unfolded Gradient Descent

Deep unfolding is a promising deep-learning technique in which an iterative algorithm is unrolled to a deep network architecture with trainable parameters. In the case of gradient descent algorithms, as a result of the training process, one often observes the acceleration of the convergence speed with learned non-constant step size parameters whose behavior is not intuitive nor interpretable from conventional theory. In this paper, we provide a theoretical interpretation of the learned step size of deep-unfolded gradient descent (DUGD). We first prove that the training process of DUGD reduces not only the mean squared error loss but also the spectral radius related to the convergence rate. Next, we show that minimizing the upper bound of the spectral radius naturally leads to the Chebyshev step which is a sequence of the step size based on Chebyshev polynomials. The numerical experiments confirm that the Chebyshev steps qualitatively reproduce the learned step size parameters in DUGD, which provides a plausible interpretation of the learned parameters. Additionally, we show that the Chebyshev steps achieve the lower bound of the convergence rate for the first-order method in a specific limit without learning parameters or momentum terms.

Trainable Projected Gradient Detector for Sparsely Spread Code Division Multiple Access

Sparsely spread code division multiple access (SCDMA) is a promising non-orthogonal multiple access technique for future wireless communications. In this paper, we propose a novel trainable multiuser detector called sparse trainable projected gradient (STPG) detector, which is based on the notion of deep unfolding. In the STPG detector, trainable parameters are embedded to a projected gradient descent algorithm, which can be trained by standard deep learning techniques such as back propagation and stochastic gradient descent. Advantages of the detector are its low computational cost and small number of trainable parameters, which enables us to treat massive SCDMA systems. In particular, its computational cost is smaller than a conventional belief propagation (BP) detector while the STPG detector exhibits nearly same detection performance with a BP detector. We also propose a scalable joint learning of signature sequences and the STPG detector for signature design. Numerical results show that the joint learning improves multiuser detection performance particular in the low SNR regime.

Complex Field-Trainable ISTA for Linear and Nonlinear Inverse Problems

Complex-field linear/nonlinear inverse problems are central issues in wireless communication systems. In this paper, we propose a novel trainable iterative signal recovery algorithm named complex-field TISTA (C-TISTA), which is an extension of recently proposed trainable iterative soft thresholding algorithm (TISTA) for real-valued compressed sensing. The proposed C-TISTA consists of a gradient step with Wirtinger derivatives, projection step with a shrinkage function, and error-variance estimator whose trainable parameters are learned by standard deep learning techniques. We examine the performance of C-TISTA in three distinct problems: complex-valued compressed sensing, discrete signal detection for an underdetermined system, and discrete signal recovery for nonlinear clipped OFDM systems. Numerical results indicate that C-TISTA provides remarkable signal recovery performance in these problems, which suggests a promising potential of C-TISTA to a wide range of inverse problems.

Trainable Projected Gradient Detector for Massive Overloaded MIMO Channels: Data-driven Tuning Approach

The paper presents a deep learning-aided iterative detection algorithm for massive overloaded multiple-input multiple-output (MIMO) systems where the number of transmit antennas $n(\gg 1)$ is larger than that of receive antennas $m$. Since the proposed algorithm is based on the projected gradient descent method with trainable parameters, it is named as the trainable projected gradient-detector (TPG-detector). The trainable internal parameters like step size parameters can be optimized with standard deep learning techniques such as back propagation and stochastic gradient descent algorithms. This approach referred to as data-driven tuning brings notable advantages of the proposed scheme such as fast convergence. The main iterative process of the TPG-detector consists of matrix-vector product operations that require $O(m n)$-time for each iterative step. In addition, the number of trainable parameters in the TPG-detector is independent of the number of antennas $n$ and $m$. These features of the TPG-detector lead to its fast and stable training process and reasonable scalability to large systems. The numerical simulations show that the proposed detector achieves comparable detection performance to those of the known algorithms for massive overloaded MIMO channels, e.g., the state-of-the-art IW-SOAV detector, with lower computation cost.