Computationally Efficient Sparse Signal Recovery via Linear Sketching and Deep Unfolding

This paper provides a sparse signal recovery algorithm, DU-PSISTA (Deep Unfolded-Periodic Sketched Iterative Shrinkage-Thresholding Algorithm), which aims to balance computational efficiency and accuracy for recovering high-dimensional sparse signals, and a convergence analysis under sufficient conditions. DU-PSISTA introduces a random matrix projection known as sketching to reduce the dimensionality of gradient computations and periodically alternates between the standard ISTA and the sketched variant. This hybrid structure enables flexible control over the trade-off between accuracy and computational complexity through a pre-configurable period parameter. The algorithm includes many parameters to be tuned such as step sizes and thresholding factors so that we incorporate deep unfolding that optimizes the parameters through data-driven training, enabling the algorithm to adaptively improve convergence speed and performance. We show that the proposed method achieves a linear-type contraction to a neighborhood of the true sparse signal with properly selected parameters. The analysis provides an interpretation for the effectiveness of the hybrid structure to improve recovery accuracy. Numerical experiments confirm that our method achieves comparable recovery performance to conventional deep unfolded ISTA while reducing computational complexity, especially when the period parameter and sketch size are properly selected. The results are also consistent with the theoretical insights.

Online Architecture Search for Compressed Sensing based on Hypergradient Descent

AS-ISTA (Architecture Searched-Iterative Shrinkage Thresholding Algorithm) and AS-FISTA (AS-Fast ISTA) are compressed sensing algorithms introducing structural parameters to ISTA and FISTA to enable architecture search within the iterative process. The structural parameters are determined using deep unfolding, but this approach requires training data and the large overhead of training time. In this paper, we propose HGD-AS-ISTA (Hypergradient Descent-AS-ISTA) and HGD-AS-FISTA that use hypergradient descent, which is an online hyperparameter optimization method, to determine the structural parameters. Experimental results show that the proposed method improves performance of the conventional ISTA/FISTA while avoiding the need for re-training when the environment changes.

Multi-Output Gaussian Processes for Graph-Structured Data

Graph-structured data is a type of data to be obtained associated with a graph structure where vertices and edges describe some kind of data correlation. This paper proposes a regression method on graph-structured data, which is based on multi-output Gaussian processes (MOGP), to capture both the correlation between vertices and the correlation between associated data. The proposed formulation is built on the definition of MOGP. This allows it to be applied to a wide range of data configurations and scenarios. Moreover, it has high expressive capability due to its flexibility in kernel design. It includes existing methods of Gaussian processes for graph-structured data as special cases and is possible to remove restrictions on data configurations, model selection, and inference scenarios in the existing methods. The performance of extensions achievable by the proposed formulation is evaluated through computer experiments with synthetic and real data.

Ordinary Differential Equation-based MIMO Signal Detection

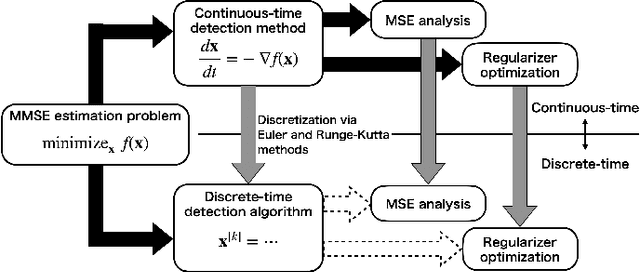
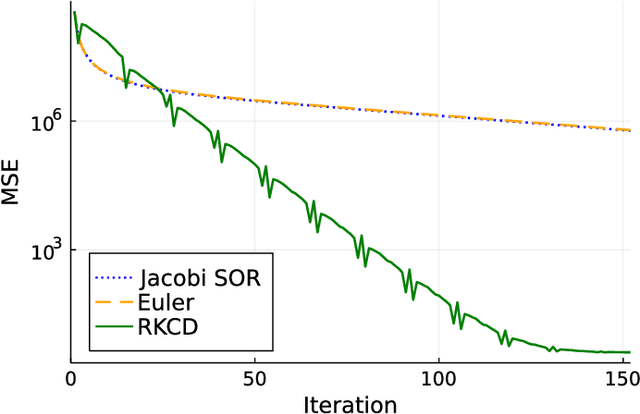
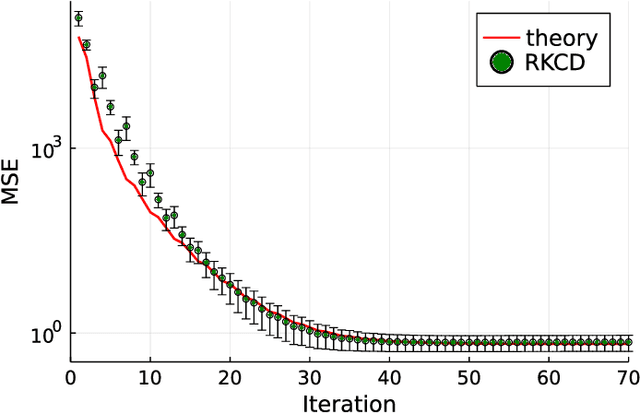
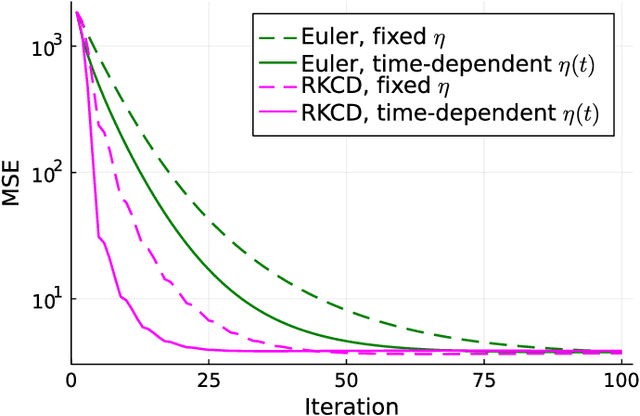
Inspired by the emerging technologies for energy-efficient analog computing and continuous-time processing, this paper proposes a continuous-time minimum mean squared error (MMSE) estimation for multiple-input multiple-output (MIMO) systems based on an ordinary differential equation (ODE). We derive an analytical formula for the mean squared error (MSE) at any given time, which is a primary performance measure for estimation methods in MIMO systems. The MSE of the proposed method depends on the regularization parameter, which affects the convergence properties. In addition, this method is extended by incorporating a time-dependent regularization parameter to enhance convergence performance. Numerical experiments demonstrate excellent consistency with theoretical values and improved convergence performance due to the integration of the time-dependent parameter. Other benefits of the ODE are also discussed in this paper. Discretizing the ODE for MMSE estimation using numerical methods provides insights into the construction and understanding of discrete-time estimation algorithms. We present discrete-time estimation algorithms based on the Euler and Runge-Kutta methods. The performance of the algorithms can be analyzed using the MSE formula for continuous-time methods, and their performance can be improved by using theoretical results in a continuous-time domain. These benefits can only be obtained through formulations using ODE.

Deep Unfolding-based Weighted Averaging for Federated Learning under Heterogeneous Environments

Federated learning is a collaborative model training method by iterating model updates at multiple clients and aggregation of the updates at a central server. Device and statistical heterogeneity of the participating clients cause performance degradation so that an appropriate weight should be assigned per client in the server's aggregation phase. This paper employs deep unfolding to learn the weights that adapt to the heterogeneity, which gives the model with high accuracy on uniform test data. The results of numerical experiments indicate the high performance of the proposed method and the interpretable behavior of the learned weights.

Energy Efficient Over-the-Air Computation for Correlated Data in Wireless Sensor Networks

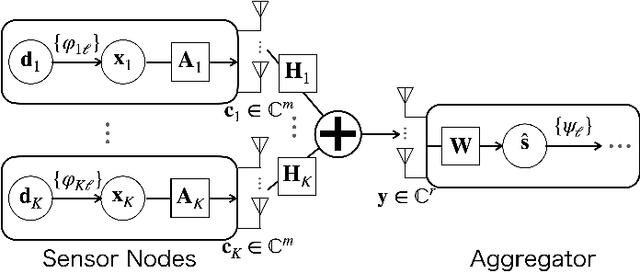
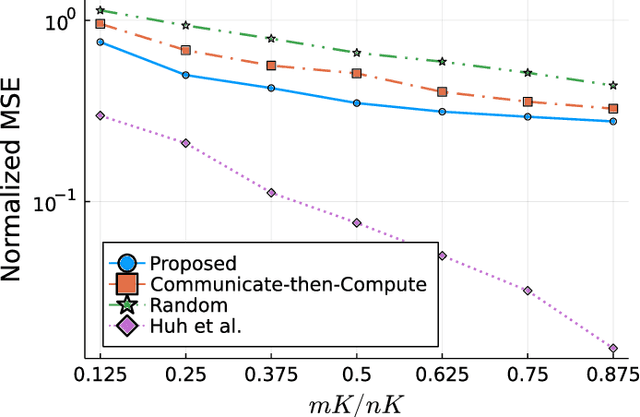
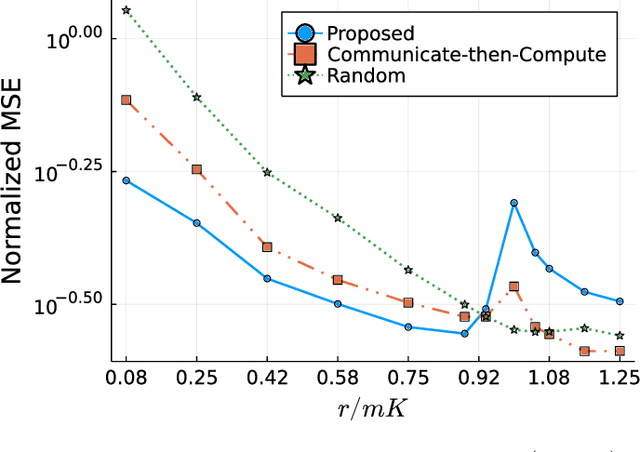
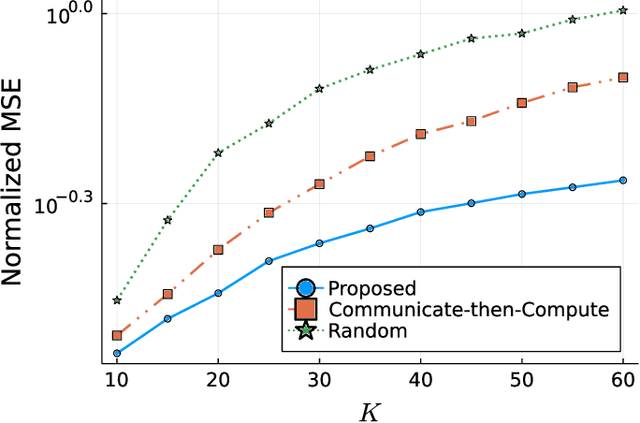
Over-the-air computation (AirComp) enables efficient wireless data aggregation in sensor networks by simultaneous processing of calculation and communication. This paper proposes a novel precoding method for AirComp that incorporates statistical properties of sensing data, spatial correlation and heterogeneous data correlation. The design of the proposed precoding matrix requires no iterative processes so that it can be realized with low computational costs. Moreover, this method provides dimensionality reduction of sensing data to reduce communication costs per sensor. We evaluate performance of the proposed method in terms of various system parameters. The results show the superiority of the proposed method to conventional non-iterative methods in cases where the number of receive antennas at the aggregator is less than that of the total transmit antennas at the sensors.

MMSE Signal Detection for MIMO Systems based on Ordinary Differential Equation

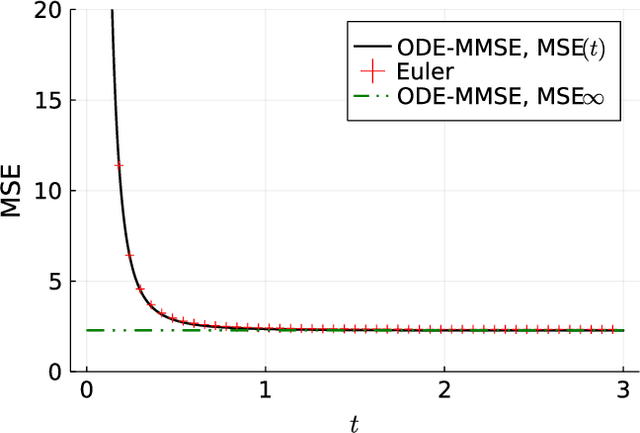
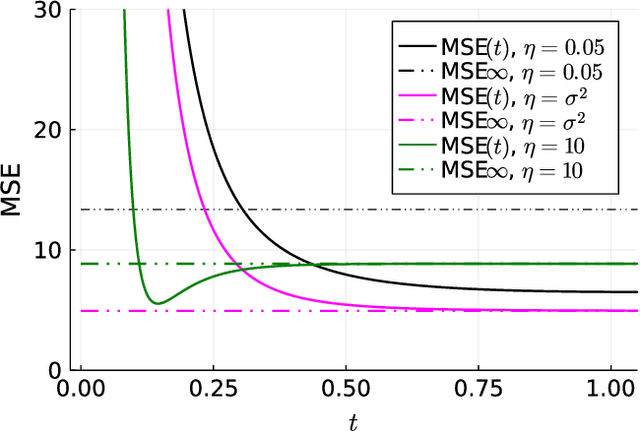
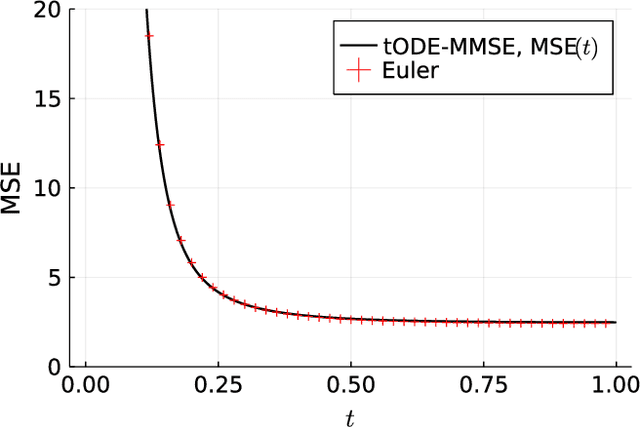
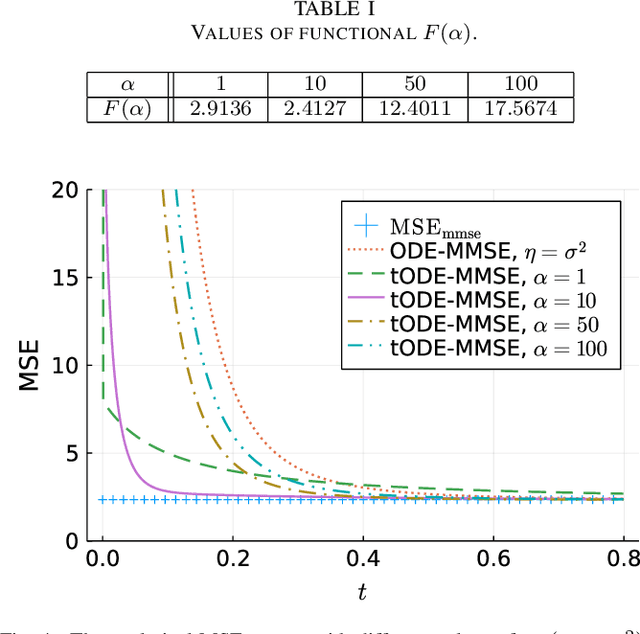
Motivated by emerging technologies for energy efficient analog computing and continuous-time processing, this paper proposes continuous-time minimum mean squared error estimation for multiple-input multiple-output (MIMO) systems based on an ordinary differential equation. Mean squared error (MSE) is a principal detection performance measure of estimation methods for MIMO systems. We derive an analytical MSE formula that indicates the MSE at any time. The MSE of the proposed method depends on a regularization parameter which affects the convergence property of the MSE. Furthermore, we extend the proposed method by using a time-dependent regularization parameter to achieve better convergence performance. Numerical experiments indicated excellent agreement with the theoretical values and improvement in the convergence performance owing to the use of the time-dependent parameter.