Ordinary Differential Equation-based MIMO Signal Detection

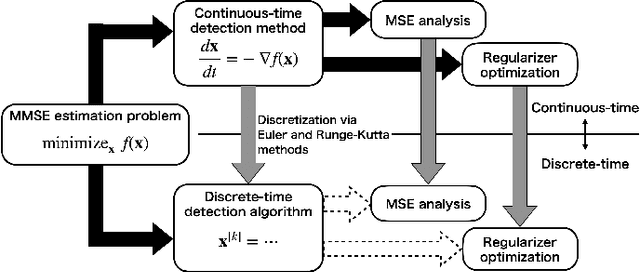
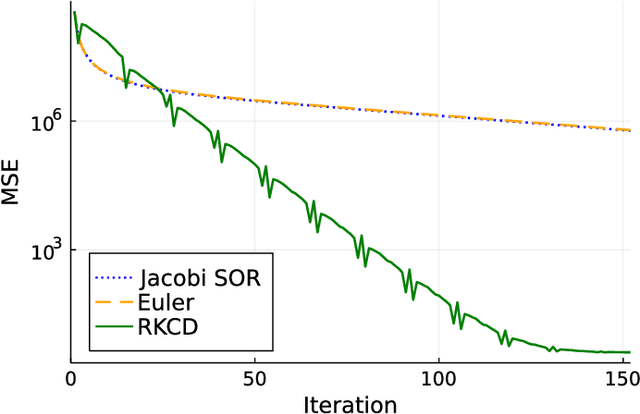
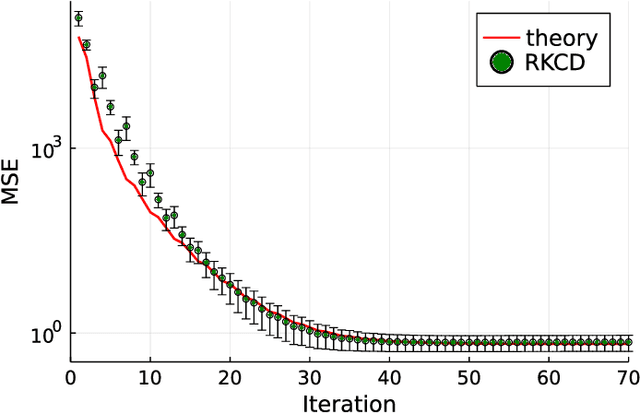
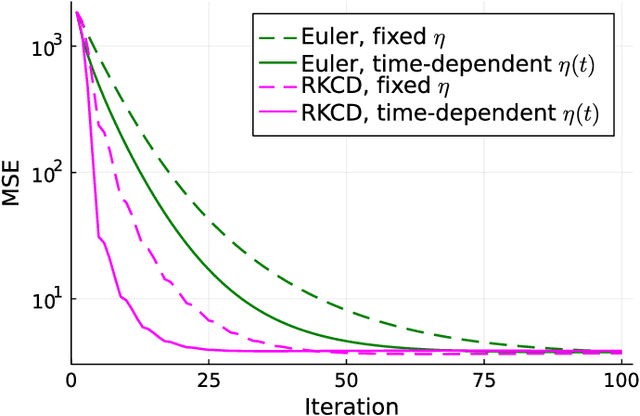
Inspired by the emerging technologies for energy-efficient analog computing and continuous-time processing, this paper proposes a continuous-time minimum mean squared error (MMSE) estimation for multiple-input multiple-output (MIMO) systems based on an ordinary differential equation (ODE). We derive an analytical formula for the mean squared error (MSE) at any given time, which is a primary performance measure for estimation methods in MIMO systems. The MSE of the proposed method depends on the regularization parameter, which affects the convergence properties. In addition, this method is extended by incorporating a time-dependent regularization parameter to enhance convergence performance. Numerical experiments demonstrate excellent consistency with theoretical values and improved convergence performance due to the integration of the time-dependent parameter. Other benefits of the ODE are also discussed in this paper. Discretizing the ODE for MMSE estimation using numerical methods provides insights into the construction and understanding of discrete-time estimation algorithms. We present discrete-time estimation algorithms based on the Euler and Runge-Kutta methods. The performance of the algorithms can be analyzed using the MSE formula for continuous-time methods, and their performance can be improved by using theoretical results in a continuous-time domain. These benefits can only be obtained through formulations using ODE.