Absorbing Phase Transitions in Artificial Deep Neural Networks

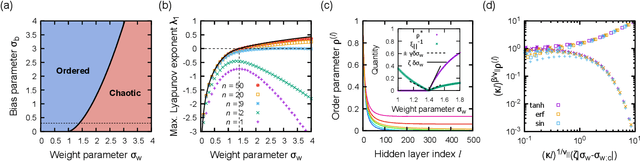
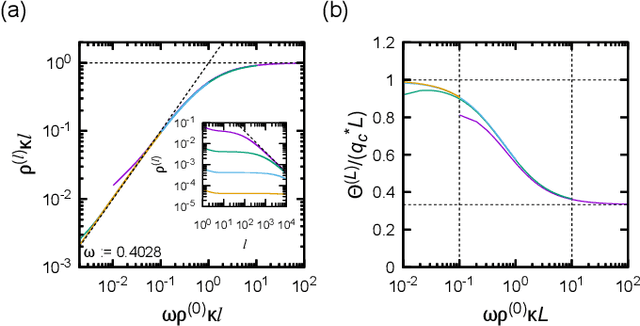
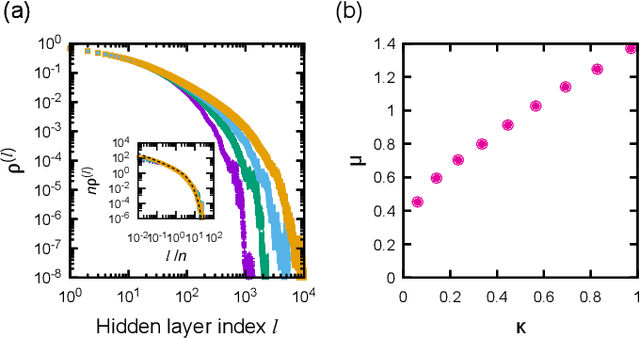
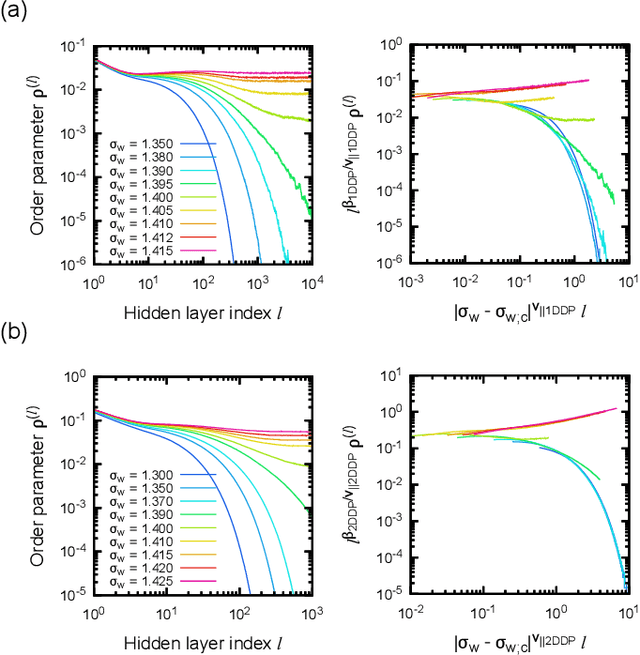
Theoretical understanding of the behavior of infinitely-wide neural networks has been rapidly developed for various architectures due to the celebrated mean-field theory. However, there is a lack of a clear, intuitive framework for extending our understanding to finite networks that are of more practical and realistic importance. In the present contribution, we demonstrate that the behavior of properly initialized neural networks can be understood in terms of universal critical phenomena in absorbing phase transitions. More specifically, we study the order-to-chaos transition in the fully-connected feedforward neural networks and the convolutional ones to show that (i) there is a well-defined transition from the ordered state to the chaotics state even for the finite networks, and (ii) difference in architecture is reflected in that of the universality class of the transition. Remarkably, the finite-size scaling can also be successfully applied, indicating that intuitive phenomenological argument could lead us to semi-quantitative description of the signal propagation dynamics.

Neural Network Approach to Construction of Classical Integrable Systems

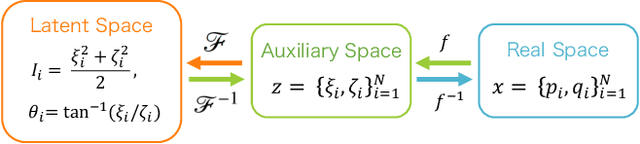
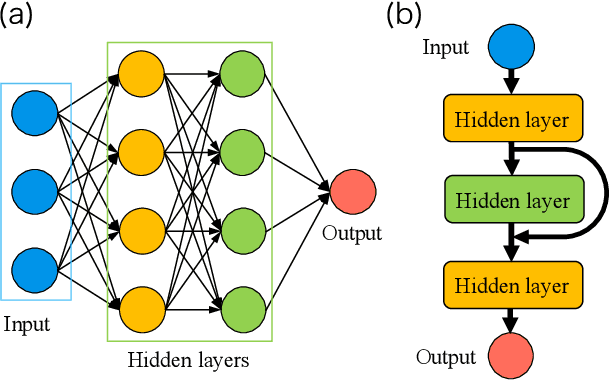
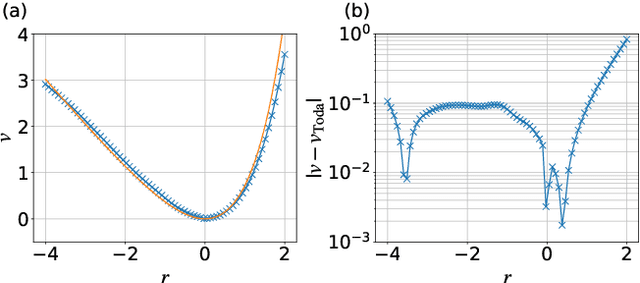
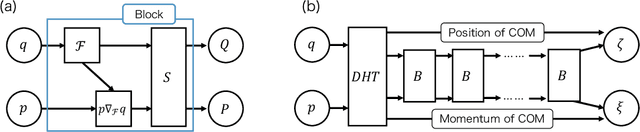
Integrable systems have provided various insights into physical phenomena and mathematics. The way of constructing many-body integrable systems is limited to few ansatzes for the Lax pair, except for highly inventive findings of conserved quantities. Machine learning techniques have recently been applied to broad physics fields and proven powerful for building non-trivial transformations and potential functions. We here propose a machine learning approach to a systematic construction of classical integrable systems. Given the Hamiltonian or samples in latent space, our neural network simultaneously learns the corresponding natural Hamiltonian in real space and the canonical transformation between the latent space and the real space variables. We also propose a loss function for building integrable systems and demonstrate successful unsupervised learning for the Toda lattice. Our approach enables exploring new integrable systems without any prior knowledge about the canonical transformation or any ansatz for the Lax pair.

Search for Common Minima in Joint Optimization of Multiple Cost Functions

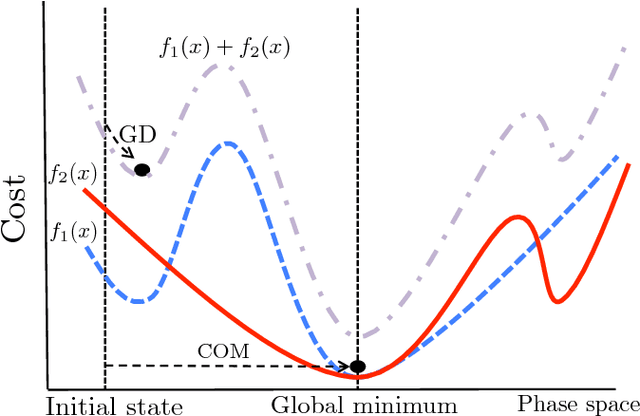
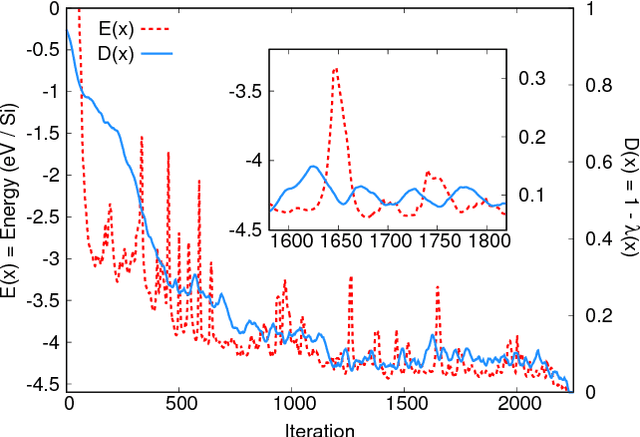
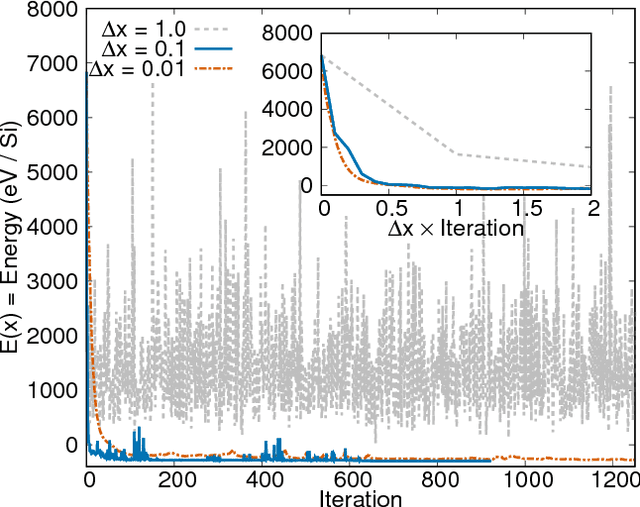
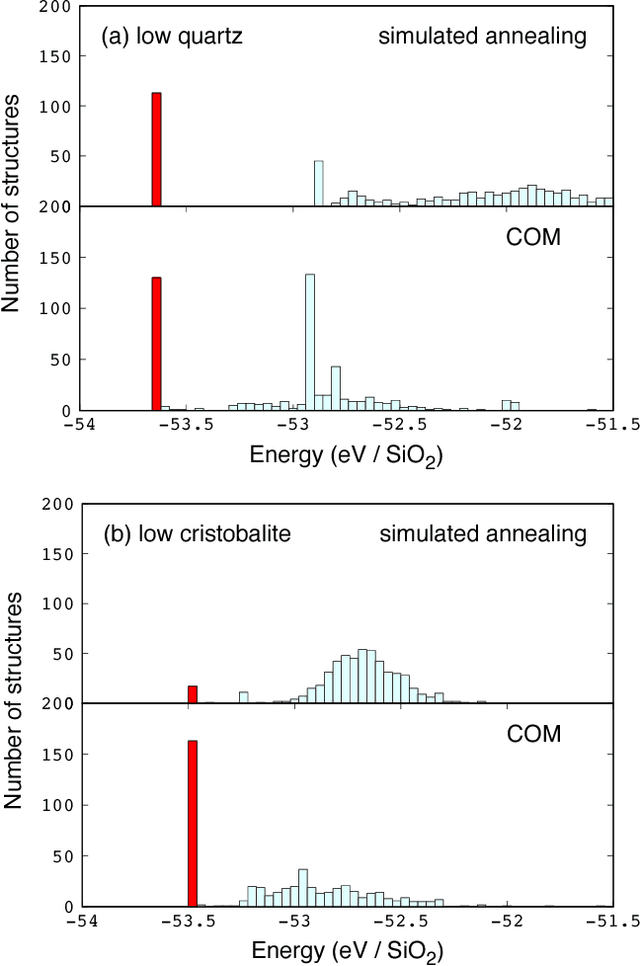
We present a novel optimization method, named the Combined Optimization Method (COM), for the joint optimization of two or more cost functions. Unlike the conventional joint optimization schemes, which try to find minima in a weighted sum of cost functions, the COM explores search space for common minima shared by all the cost functions. Given a set of multiple cost functions that have qualitatively different distributions of local minima with each other, the proposed method finds the common minima with a high success rate without the help of any metaheuristics. As a demonstration, we apply the COM to the crystal structure prediction in materials science. By introducing the concept of data assimilation, i.e., adopting the theoretical potential energy of the crystal and the crystallinity, which characterizes the agreement with the theoretical and experimental X-ray diffraction patterns, as cost functions, we show that the correct crystal structures of Si diamond, low quartz, and low cristobalite can be predicted with significantly higher success rates than the previous methods.