Plastic tensor networks for interpretable generative modeling

A structural optimization scheme for a single-layer nonnegative adaptive tensor tree (NATT) that models a target probability distribution is proposed. The NATT scheme, by construction, has the advantage that it is interpretable as a probabilistic graphical model. We consider the NATT scheme and a recently proposed Born machine adaptive tensor tree (BMATT) optimization scheme and demonstrate their effectiveness on a variety of generative modeling tasks where the objective is to infer the hidden structure of a provided dataset. Our results show that in terms of minimizing the negative log-likelihood, the single-layer scheme has model performance comparable to the Born machine scheme, though not better. The tasks include deducing the structure of binary bitwise operations, learning the internal structure of random Bayesian networks given only visible sites, and a real-world example related to hierarchical clustering where a cladogram is constructed from mitochondrial DNA sequences. In doing so, we also show the importance of the choice of network topology and the versatility of a least-mutual information criterion in selecting a candidate structure for a tensor tree, as well as discuss aspects of these tensor tree generative models including their information content and interpretability.

Tensor tree learns hidden relational structures in data to construct generative models

Based on the tensor tree network with the Born machine framework, we propose a general method for constructing a generative model by expressing the target distribution function as the quantum wave function amplitude represented by a tensor tree. The key idea is dynamically optimizing the tree structure that minimizes the bond mutual information. The proposed method offers enhanced performance and uncovers hidden relational structures in the target data. We illustrate potential practical applications with four examples: (i) random patterns, (ii) QMNIST hand-written digits, (iii) Bayesian networks, and (iv) the stock price fluctuation pattern in S&P500. In (i) and (ii), strongly correlated variables were concentrated near the center of the network; in (iii), the causality pattern was identified; and, in (iv), a structure corresponding to the eleven sectors emerged.

Absorbing Phase Transitions in Artificial Deep Neural Networks

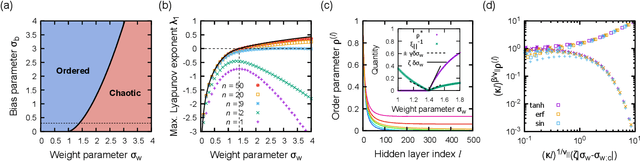
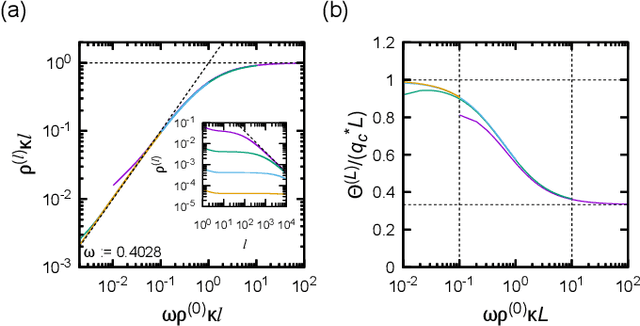
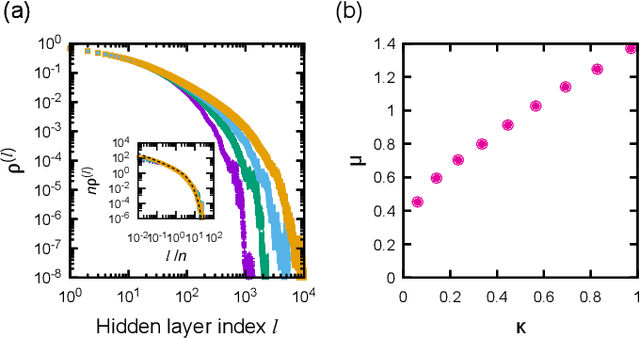
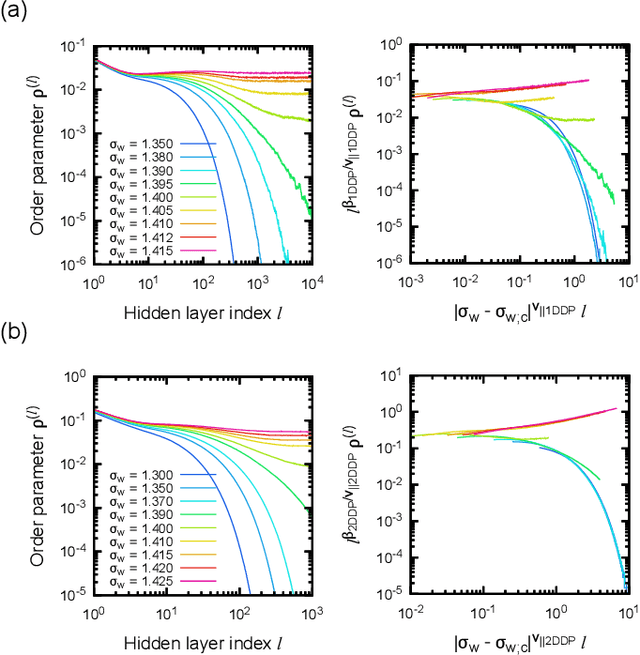
Theoretical understanding of the behavior of infinitely-wide neural networks has been rapidly developed for various architectures due to the celebrated mean-field theory. However, there is a lack of a clear, intuitive framework for extending our understanding to finite networks that are of more practical and realistic importance. In the present contribution, we demonstrate that the behavior of properly initialized neural networks can be understood in terms of universal critical phenomena in absorbing phase transitions. More specifically, we study the order-to-chaos transition in the fully-connected feedforward neural networks and the convolutional ones to show that (i) there is a well-defined transition from the ordered state to the chaotics state even for the finite networks, and (ii) difference in architecture is reflected in that of the universality class of the transition. Remarkably, the finite-size scaling can also be successfully applied, indicating that intuitive phenomenological argument could lead us to semi-quantitative description of the signal propagation dynamics.