Absorbing Phase Transitions in Artificial Deep Neural Networks
Paper and Code
Jul 05, 2023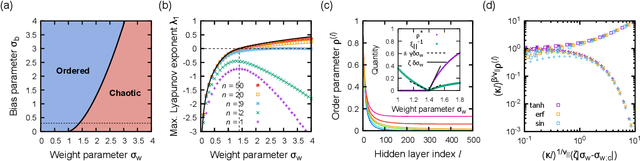
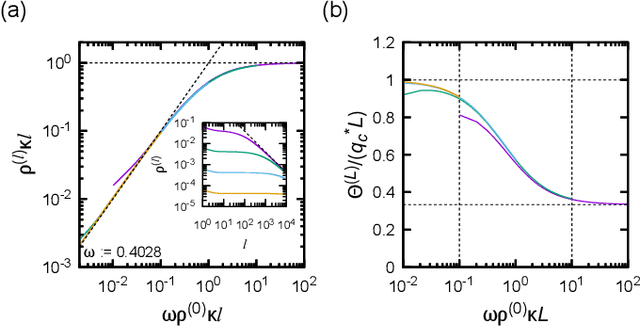
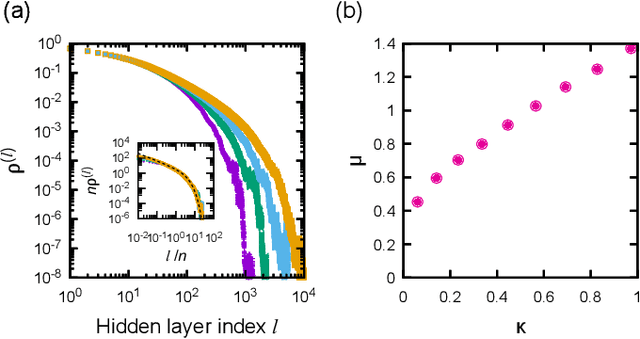
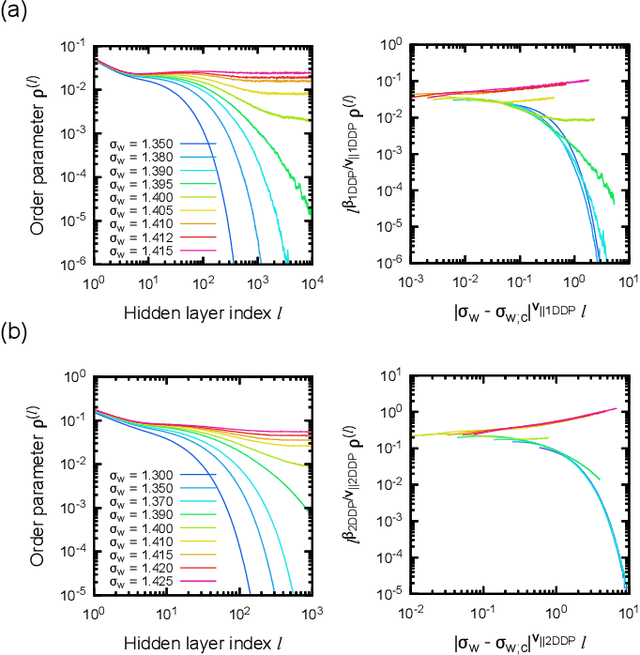
Theoretical understanding of the behavior of infinitely-wide neural networks has been rapidly developed for various architectures due to the celebrated mean-field theory. However, there is a lack of a clear, intuitive framework for extending our understanding to finite networks that are of more practical and realistic importance. In the present contribution, we demonstrate that the behavior of properly initialized neural networks can be understood in terms of universal critical phenomena in absorbing phase transitions. More specifically, we study the order-to-chaos transition in the fully-connected feedforward neural networks and the convolutional ones to show that (i) there is a well-defined transition from the ordered state to the chaotics state even for the finite networks, and (ii) difference in architecture is reflected in that of the universality class of the transition. Remarkably, the finite-size scaling can also be successfully applied, indicating that intuitive phenomenological argument could lead us to semi-quantitative description of the signal propagation dynamics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge