Search for Common Minima in Joint Optimization of Multiple Cost Functions
Paper and Code
Aug 21, 2018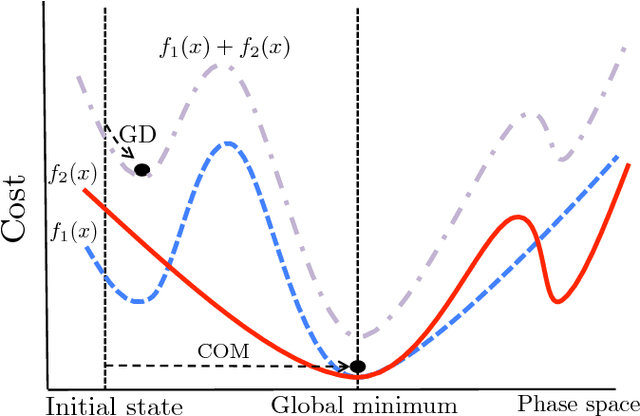
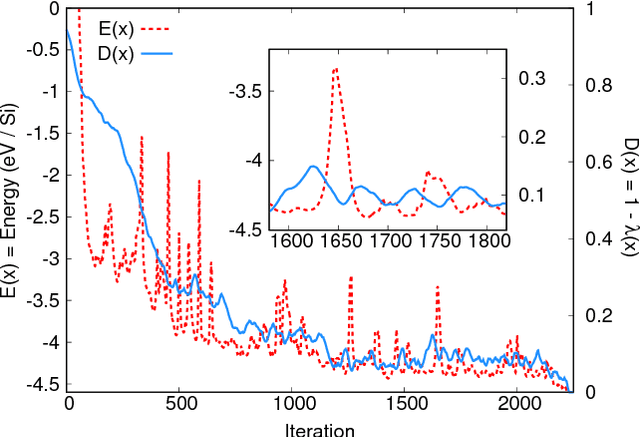
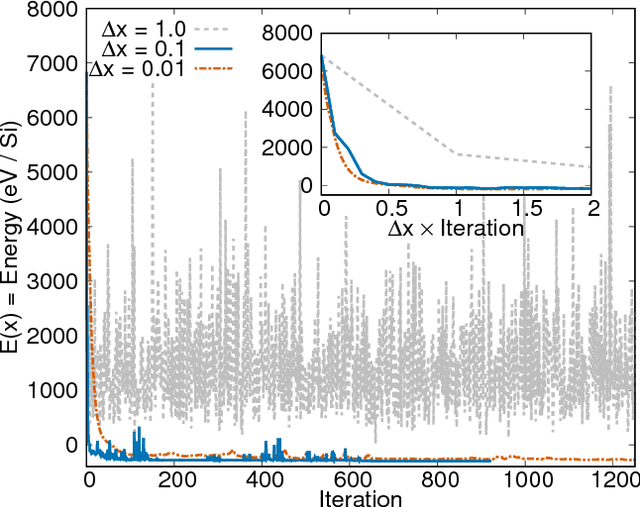
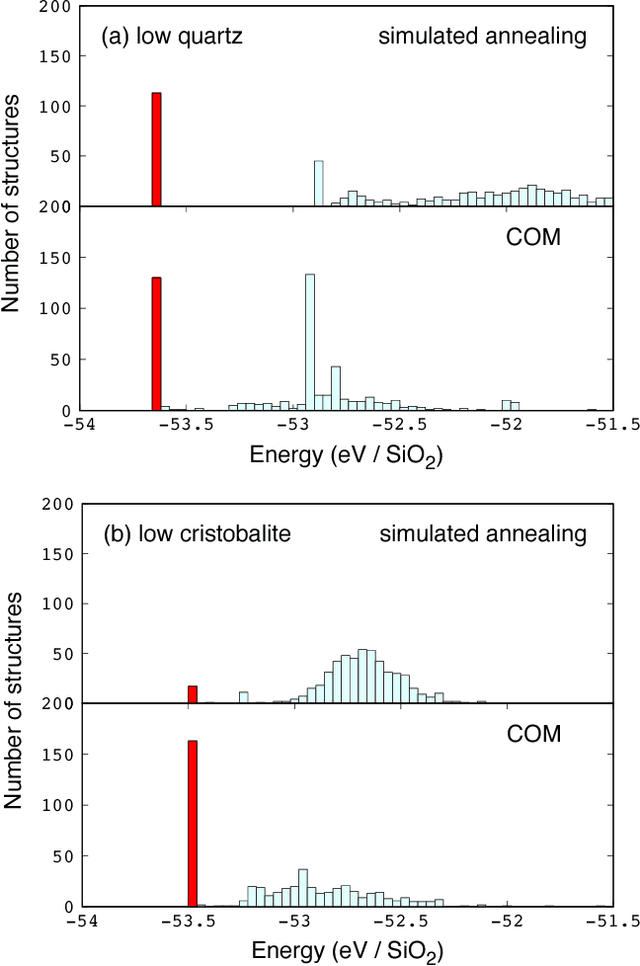
We present a novel optimization method, named the Combined Optimization Method (COM), for the joint optimization of two or more cost functions. Unlike the conventional joint optimization schemes, which try to find minima in a weighted sum of cost functions, the COM explores search space for common minima shared by all the cost functions. Given a set of multiple cost functions that have qualitatively different distributions of local minima with each other, the proposed method finds the common minima with a high success rate without the help of any metaheuristics. As a demonstration, we apply the COM to the crystal structure prediction in materials science. By introducing the concept of data assimilation, i.e., adopting the theoretical potential energy of the crystal and the crystallinity, which characterizes the agreement with the theoretical and experimental X-ray diffraction patterns, as cost functions, we show that the correct crystal structures of Si diamond, low quartz, and low cristobalite can be predicted with significantly higher success rates than the previous methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge