Sylvain Courtain
Relative Entropy-Regularized Optimal Transport on a Graph: a new algorithm and an experimental comparison
Aug 23, 2021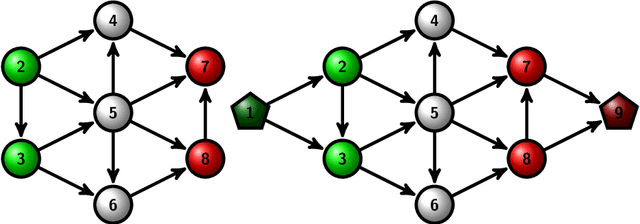
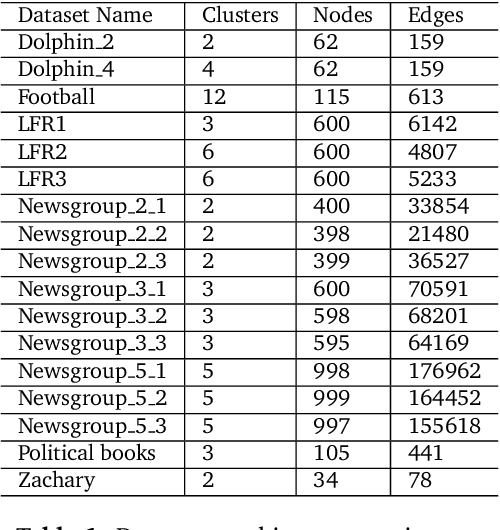
Abstract:Following [21, 23], the present work investigates a new relative entropy-regularized algorithm for solving the optimal transport on a graph problem within the randomized shortest paths formalism. More precisely, a unit flow is injected into a set of input nodes and collected from a set of output nodes while minimizing the expected transportation cost together with a paths relative entropy regularization term, providing a randomized routing policy. The main advantage of this new formulation is the fact that it can easily accommodate edge flow capacity constraints which commonly occur in real-world problems. The resulting optimal routing policy, i.e., the probability distribution of following an edge in each node, is Markovian and is computed by constraining the input and output flows to the prescribed marginal probabilities thanks to a variant of the algorithm developed in [8]. Besides, experimental comparisons with other recently developed techniques show that the distance measure between nodes derived from the introduced model provides competitive results on semi-supervised classification tasks.
Sparse Randomized Shortest Paths Routing with Tsallis Divergence Regularization
Jul 01, 2020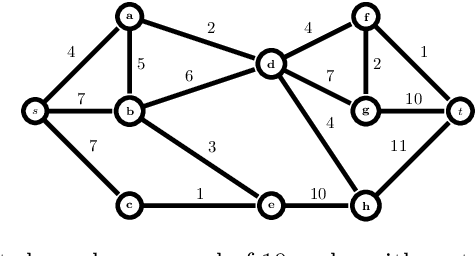


Abstract:This work elaborates on the important problem of (1) designing optimal randomized routing policies for reaching a target node t from a source note s on a weighted directed graph G and (2) defining distance measures between nodes interpolating between the least cost (based on optimal movements) and the commute-cost (based on a random walk on G), depending on a temperature parameter T. To this end, the randomized shortest path formalism (RSP, [2,99,124]) is rephrased in terms of Tsallis divergence regularization, instead of Kullback-Leibler divergence. The main consequence of this change is that the resulting routing policy (local transition probabilities) becomes sparser when T decreases, therefore inducing a sparse random walk on G converging to the least-cost directed acyclic graph when T tends to 0. Experimental comparisons on node clustering and semi-supervised classification tasks show that the derived dissimilarity measures based on expected routing costs provide state-of-the-art results. The sparse RSP is therefore a promising model of movements on a graph, balancing sparse exploitation and exploration in an optimal way.
Randomized Shortest Paths with Net Flows and Capacity Constraints
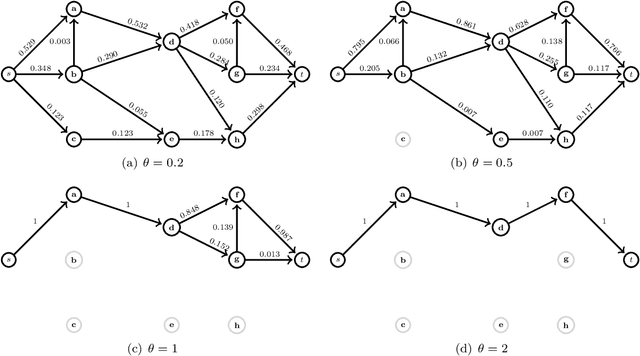
Oct 04, 2019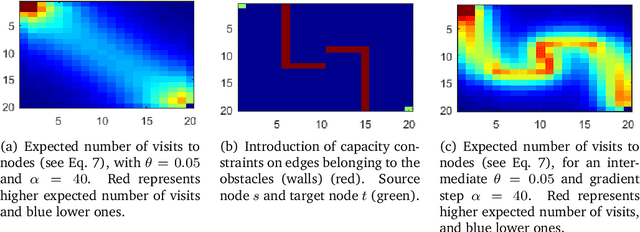
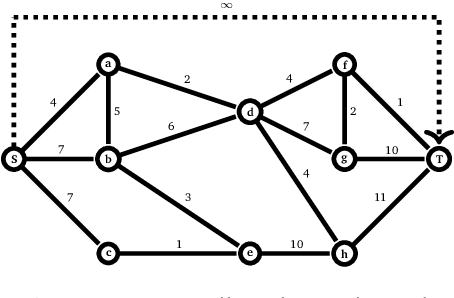
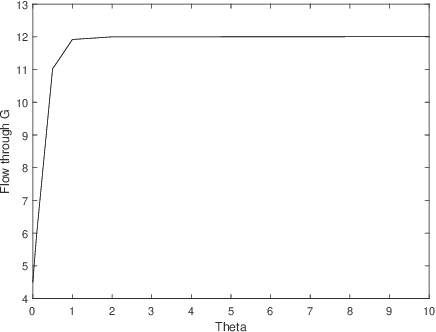
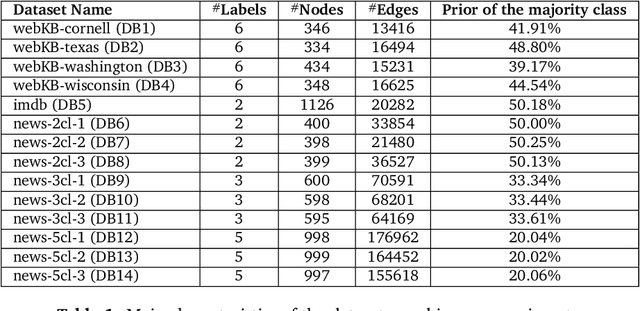
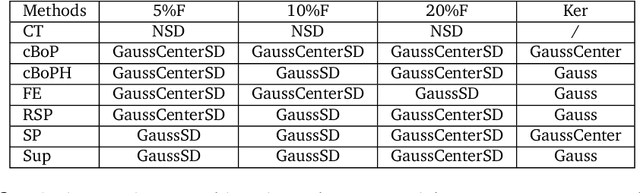
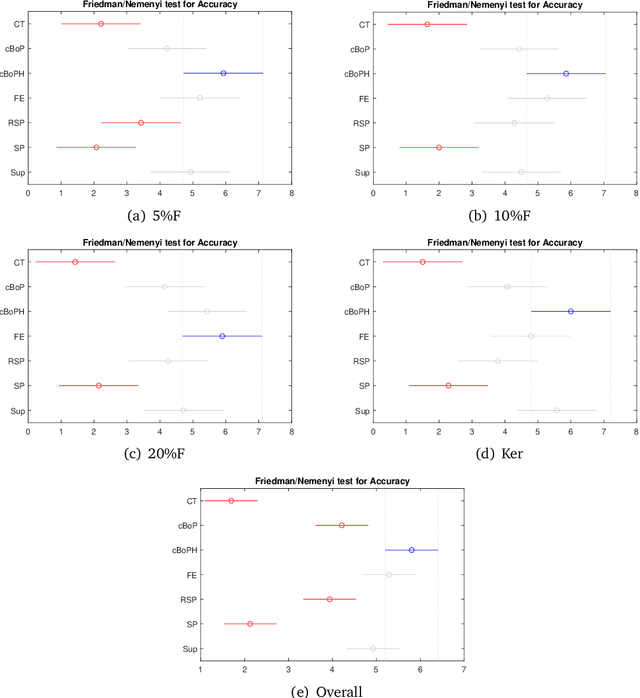
Abstract:This work extends the randomized shortest paths model (RSP) by investigating the net flow RSP and adding capacity constraints on edge flows. The standard RSP is a model of movement, or spread, through a network interpolating between a random walk and a shortest path behavior. This framework assumes a unit flow injected into a source node and collected from a target node with flows minimizing the expected transportation cost together with a relative entropy regularization term. In this context, the present work first develops the net flow RSP model considering that edge flows in opposite directions neutralize each other (as in electrical networks) and proposes an algorithm for computing the expected routing costs between all pairs of nodes. This quantity is called the net flow RSP dissimilarity measure between nodes. Experimental comparisons on node clustering tasks show that the net flow RSP dissimilarity is competitive with other state-of-the-art techniques. In the second part of the paper, it is shown how to introduce capacity constraints on edge flows and a procedure solving this constrained problem by using Lagrangian duality is developed. These two extensions improve significantly the scope of applications of the RSP framework.
Covariance and Correlation Kernels on a Graph in the Generalized Bag-of-Paths Formalism
Feb 08, 2019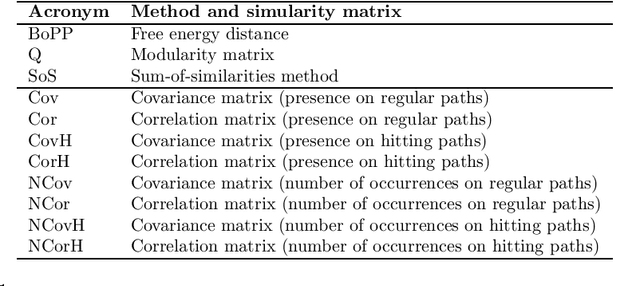
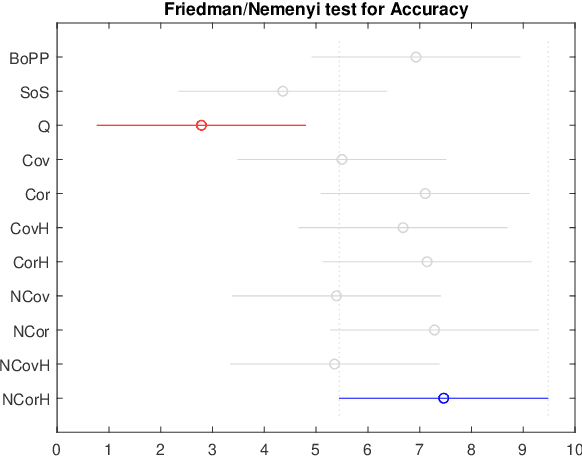
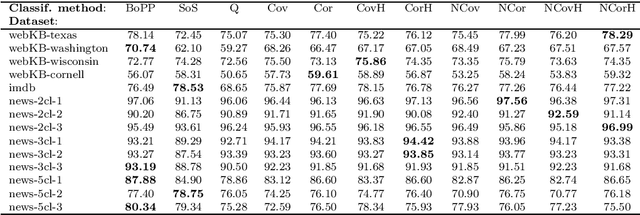
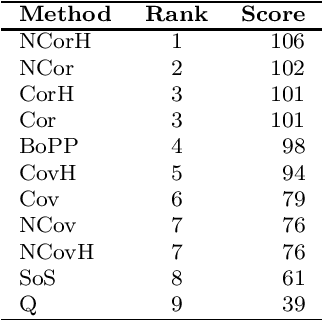
Abstract:This work derives closed-form expressions computing the expectation of co-presences and of number of co-occurences of nodes on paths sampled from a network according to general path weights (a bag of paths). The underlying idea is that two nodes are considered as similar when they appear together on (preferably short) paths of the network. The results are obtained for both regular and hitting paths and serve as a basis for computing new covariance and correlation measures between nodes. Experiments on semi-supervised classification show that the introduced similarity measures provide competitive performances compared to other state-of-the-art distances and similarities.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge