Sparse Randomized Shortest Paths Routing with Tsallis Divergence Regularization
Paper and Code
Jul 01, 2020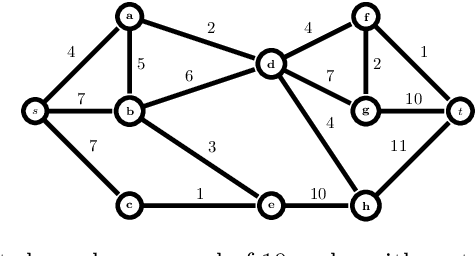

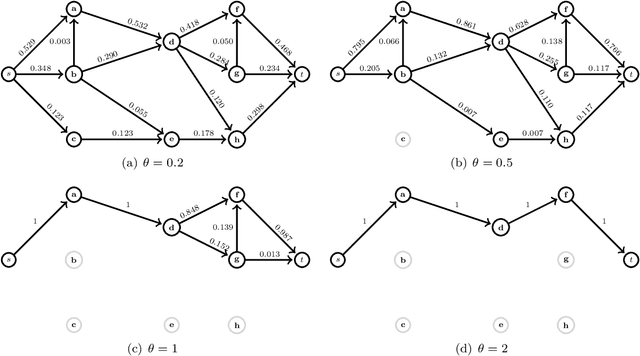

This work elaborates on the important problem of (1) designing optimal randomized routing policies for reaching a target node t from a source note s on a weighted directed graph G and (2) defining distance measures between nodes interpolating between the least cost (based on optimal movements) and the commute-cost (based on a random walk on G), depending on a temperature parameter T. To this end, the randomized shortest path formalism (RSP, [2,99,124]) is rephrased in terms of Tsallis divergence regularization, instead of Kullback-Leibler divergence. The main consequence of this change is that the resulting routing policy (local transition probabilities) becomes sparser when T decreases, therefore inducing a sparse random walk on G converging to the least-cost directed acyclic graph when T tends to 0. Experimental comparisons on node clustering and semi-supervised classification tasks show that the derived dissimilarity measures based on expected routing costs provide state-of-the-art results. The sparse RSP is therefore a promising model of movements on a graph, balancing sparse exploitation and exploration in an optimal way.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge