Relative Entropy-Regularized Optimal Transport on a Graph: a new algorithm and an experimental comparison

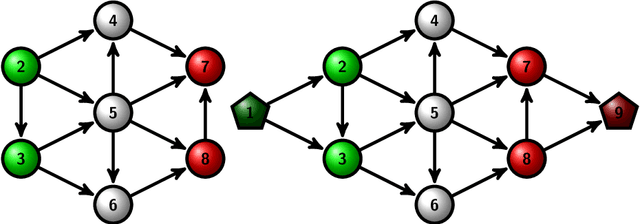
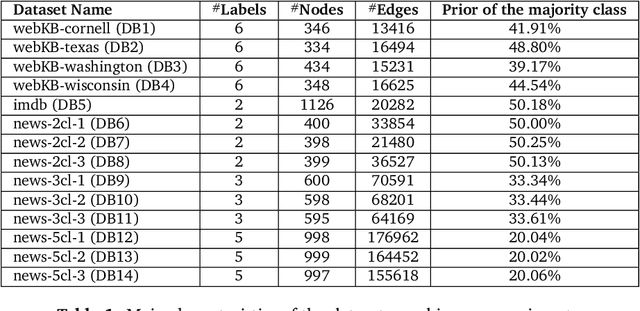
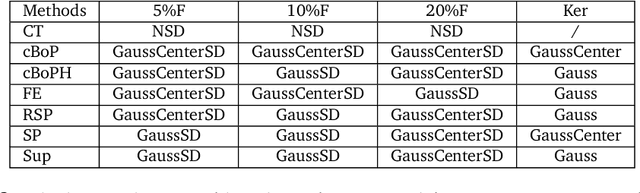
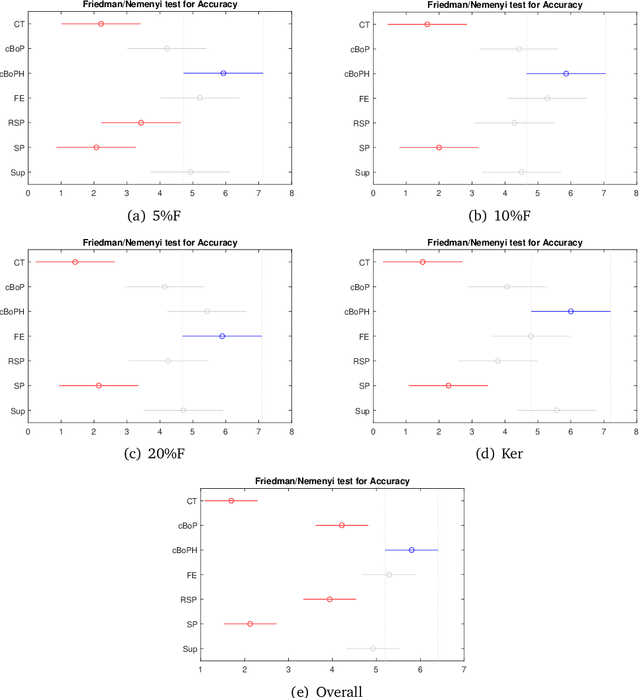
Following [21, 23], the present work investigates a new relative entropy-regularized algorithm for solving the optimal transport on a graph problem within the randomized shortest paths formalism. More precisely, a unit flow is injected into a set of input nodes and collected from a set of output nodes while minimizing the expected transportation cost together with a paths relative entropy regularization term, providing a randomized routing policy. The main advantage of this new formulation is the fact that it can easily accommodate edge flow capacity constraints which commonly occur in real-world problems. The resulting optimal routing policy, i.e., the probability distribution of following an edge in each node, is Markovian and is computed by constraining the input and output flows to the prescribed marginal probabilities thanks to a variant of the algorithm developed in [8]. Besides, experimental comparisons with other recently developed techniques show that the distance measure between nodes derived from the introduced model provides competitive results on semi-supervised classification tasks.

Randomized Shortest Paths with Net Flows and Capacity Constraints

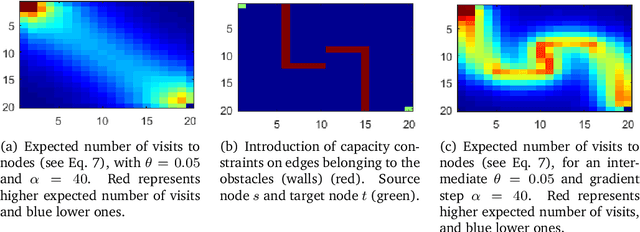
This work extends the randomized shortest paths model (RSP) by investigating the net flow RSP and adding capacity constraints on edge flows. The standard RSP is a model of movement, or spread, through a network interpolating between a random walk and a shortest path behavior. This framework assumes a unit flow injected into a source node and collected from a target node with flows minimizing the expected transportation cost together with a relative entropy regularization term. In this context, the present work first develops the net flow RSP model considering that edge flows in opposite directions neutralize each other (as in electrical networks) and proposes an algorithm for computing the expected routing costs between all pairs of nodes. This quantity is called the net flow RSP dissimilarity measure between nodes. Experimental comparisons on node clustering tasks show that the net flow RSP dissimilarity is competitive with other state-of-the-art techniques. In the second part of the paper, it is shown how to introduce capacity constraints on edge flows and a procedure solving this constrained problem by using Lagrangian duality is developed. These two extensions improve significantly the scope of applications of the RSP framework.