Collaborative AI Agents and Critics for Fault Detection and Cause Analysis in Network Telemetry

We develop algorithms for collaborative control of AI agents and critics in a multi-actor, multi-critic federated multi-agent system. Each AI agent and critic has access to classical machine learning or generative AI foundation models. The AI agents and critics collaborate with a central server to complete multimodal tasks such as fault detection, severity, and cause analysis in a network telemetry system, text-to-image generation, video generation, healthcare diagnostics from medical images and patient records, etcetera. The AI agents complete their tasks and send them to AI critics for evaluation. The critics then send feedback to agents to improve their responses. Collaboratively, they minimize the overall cost to the system with no inter-agent or inter-critic communication. AI agents and critics keep their cost functions or derivatives of cost functions private. Using multi-time scale stochastic approximation techniques, we provide convergence guarantees on the time-average active states of AI agents and critics. The communication overhead is a little on the system, of the order of $\mathcal{O}(m)$, for $m$ modalities and is independent of the number of AI agents and critics. Finally, we present an example of fault detection, severity, and cause analysis in network telemetry and thorough evaluation to check the algorithm's efficacy.

Near-optimal Differentially Private Client Selection in Federated Settings

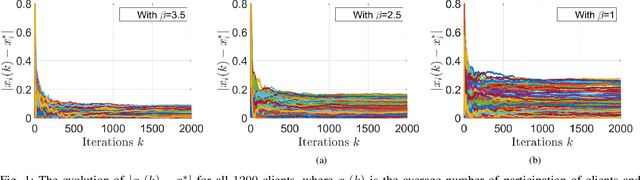
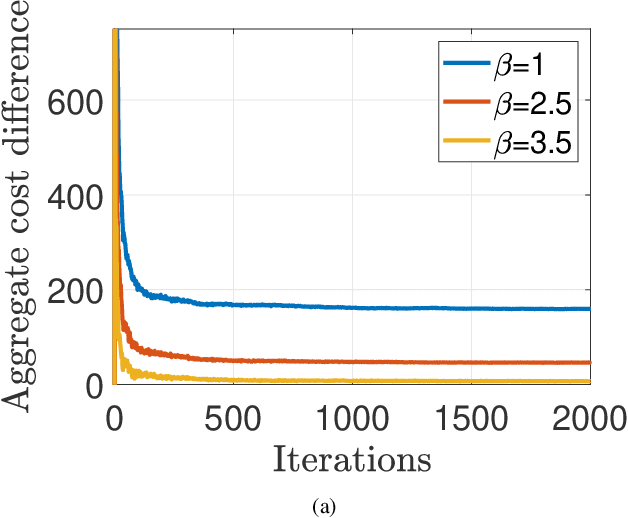
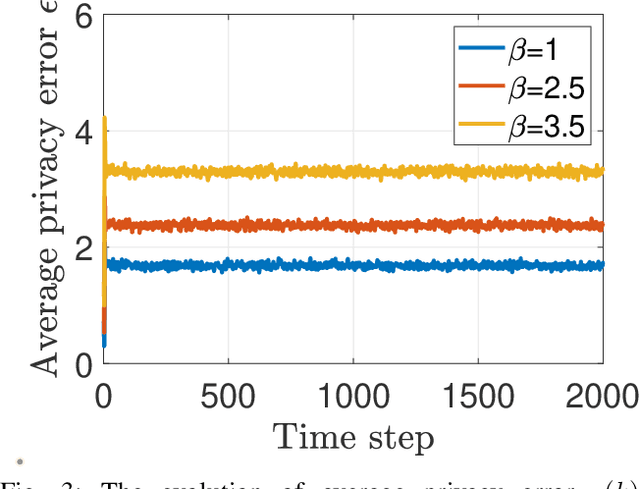
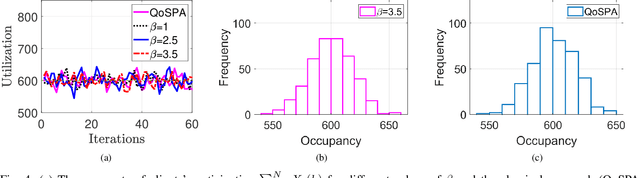
We develop an iterative differentially private algorithm for client selection in federated settings. We consider a federated network wherein clients coordinate with a central server to complete a task; however, the clients decide whether to participate or not at a time step based on their preferences -- local computation and probabilistic intent. The algorithm does not require client-to-client information exchange. The developed algorithm provides near-optimal values to the clients over long-term average participation with a certain differential privacy guarantee. Finally, we present the experimental results to check the algorithm's efficacy.

Multi-resource allocation for federated settings: A non-homogeneous Markov chain model

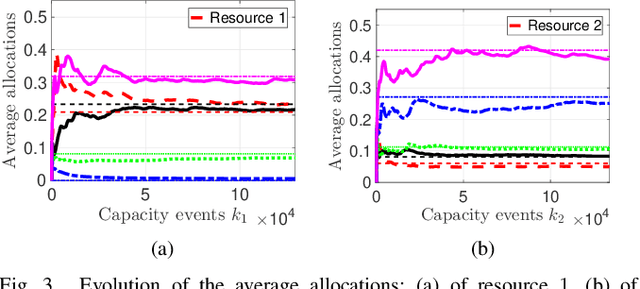
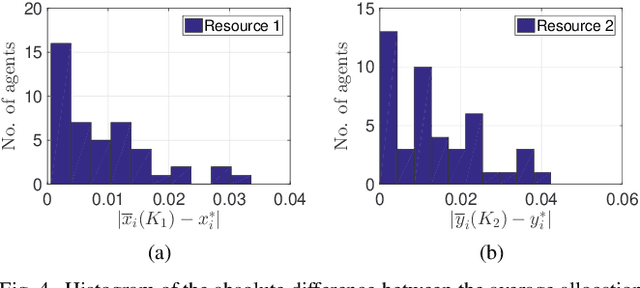
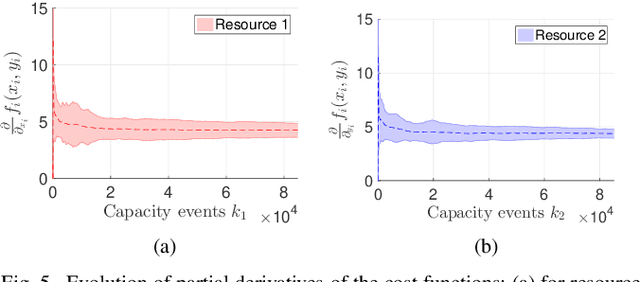
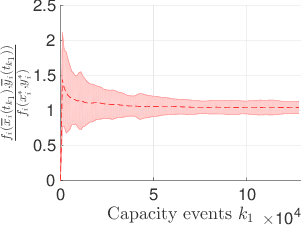
In a federated setting, agents coordinate with a central agent or a server to solve an optimization problem in which agents do not share their information with each other. Wirth and his co-authors, in a recent paper, describe how the basic additive-increase multiplicative-decrease (AIMD) algorithm can be modified in a straightforward manner to solve a class of optimization problems for federated settings for a single shared resource with no inter-agent communication. The AIMD algorithm is one of the most successful distributed resource allocation algorithms currently deployed in practice. It is best known as the backbone of the Internet and is also widely explored in other application areas. We extend the single-resource algorithm to multiple heterogeneous shared resources that emerge in smart cities, sharing economy, and many other applications. Our main results show the convergence of the average allocations to the optimal values. We model the system as a non-homogeneous Markov chain with place-dependent probabilities. Furthermore, simulation results are presented to demonstrate the efficacy of the algorithms and to highlight the main features of our analysis.