Qubit-efficient Variational Quantum Algorithms for Image Segmentation

Quantum computing is expected to transform a range of computational tasks beyond the reach of classical algorithms. In this work, we examine the application of variational quantum algorithms (VQAs) for unsupervised image segmentation to partition images into separate semantic regions. Specifically, we formulate the task as a graph cut optimization problem and employ two established qubit-efficient VQAs, which we refer to as Parametric Gate Encoding (PGE) and Ancilla Basis Encoding (ABE), to find the optimal segmentation mask. In addition, we propose Adaptive Cost Encoding (ACE), a new approach that leverages the same circuit architecture as ABE but adopts a problem-dependent cost function. We benchmark PGE, ABE and ACE on synthetically generated images, focusing on quality and trainability. ACE shows consistently faster convergence in training the parameterized quantum circuits in comparison to PGE and ABE. Furthermore, we provide a theoretical analysis of the scalability of these approaches against the Quantum Approximate Optimization Algorithm (QAOA), showing a significant cutback in the quantum resources, especially in the number of qubits that logarithmically depends on the number of pixels. The results validate the strengths of ACE, while concurrently highlighting its inherent limitations and challenges. This paves way for further research in quantum-enhanced computer vision.

Q-Seg: Quantum Annealing-based Unsupervised Image Segmentation

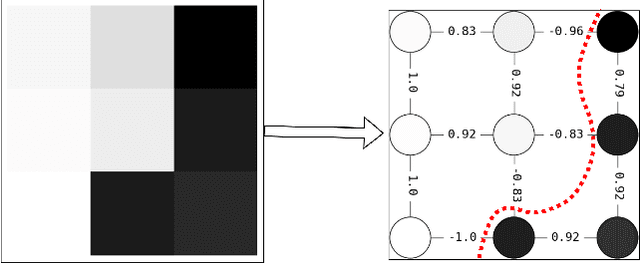
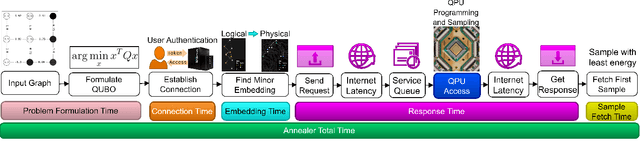
In this study, we present Q-Seg, a novel unsupervised image segmentation method based on quantum annealing, tailored for existing quantum hardware. We formulate the pixel-wise segmentation problem, which assimilates spectral and spatial information of the image, as a graph-cut optimization task. Our method efficiently leverages the interconnected qubit topology of the D-Wave Advantage device, offering superior scalability over existing quantum approaches and outperforming state-of-the-art classical methods. Our empirical evaluations on synthetic datasets reveal that Q-Seg offers better runtime performance against the classical optimizer Gurobi. Furthermore, we evaluate our method on segmentation of Earth Observation images, an area of application where the amount of labeled data is usually very limited. In this case, Q-Seg demonstrates near-optimal results in flood mapping detection with respect to classical supervised state-of-the-art machine learning methods. Also, Q-Seg provides enhanced segmentation for forest coverage compared to existing annotated masks. Thus, Q-Seg emerges as a viable alternative for real-world applications using available quantum hardware, particularly in scenarios where the lack of labeled data and computational runtime are critical.

GCS-Q: Quantum Graph Coalition Structure Generation

The problem of generating an optimal coalition structure for a given coalition game of rational agents is to find a partition that maximizes their social welfare and is known to be NP-hard. This paper proposes GCS-Q, a novel quantum-supported solution for Induced Subgraph Games (ISGs) in coalition structure generation. GCS-Q starts by considering the grand coalition as initial coalition structure and proceeds by iteratively splitting the coalitions into two nonempty subsets to obtain a coalition structure with a higher coalition value. In particular, given an $n$-agent ISG, the GCS-Q solves the optimal split problem $\mathcal{O} (n)$ times using a quantum annealing device, exploring $\mathcal{O}(2^n)$ partitions at each step. We show that GCS-Q outperforms the currently best classical solvers with its runtime in the order of $n^2$ and an expected worst-case approximation ratio of $93\%$ on standard benchmark datasets.

BILP-Q: Quantum Coalition Structure Generation

Quantum AI is an emerging field that uses quantum computing to solve typical complex problems in AI. In this work, we propose BILP-Q, the first-ever general quantum approach for solving the Coalition Structure Generation problem (CSGP), which is notably NP-hard. In particular, we reformulate the CSGP in terms of a Quadratic Binary Combinatorial Optimization (QUBO) problem to leverage existing quantum algorithms (e.g., QAOA) to obtain the best coalition structure. Thus, we perform a comparative analysis in terms of time complexity between the proposed quantum approach and the most popular classical baselines. Furthermore, we consider standard benchmark distributions for coalition values to test the BILP-Q on small-scale experiments using the IBM Qiskit environment. Finally, since QUBO problems can be solved operating with quantum annealing, we run BILP-Q on medium-size problems using a real quantum annealer (D-Wave).