Low Complexity Sequential Search with Measurement Dependent Noise

This paper considers a target localization problem where at any given time an agent can choose a region to query for the presence of the target in that region. The measurement noise is assumed to be increasing with the size of the query region the agent chooses. Motivated by practical applications such as initial beam alignment in array processing, heavy hitter detection in networking, and visual search in robotics, we consider practically important complexity constraints/metrics: \textit{time complexity}, \textit{computational and memory complexity}, \textit{query geometry}, and \textit{cardinality of possible query sets}. Two novel search strategy, $dyaPM$ and $hiePM$, are proposed. In contrast to previously proposed algorithms, $dyaPM$ and $hiePM$ are of a connected query geometry (i.e. query set is always a connected set). We also demonstrated how they can be implemented with low computational and memory complexity. Additionally, $hiePM$ has a hierarchical structure and has a low cardinality of possible query sets. These make $hiePM$ suitable for applications such as beamforming in array processing where the extra computation of the query set construction dictates a codebook-based approach (the choice of query set is constrained to a pre-computed small query set collection), and the limit of memory enforces a smaller codebook size. Through a unified analysis with Extrinsic Jensen Shannon (EJS) Divergence, $dyaPM$ is shown to be asymptotically optimal in search time complexity (asymptotic in both resolution (rate) and error (reliability)). On the other hand, $hiePM$ is shown to be near-optimal in rate. In addition, via numerical examples, both $hiePM$ and $dyaPM$ are shown to outperform prior work in the non-asymptotic regime.

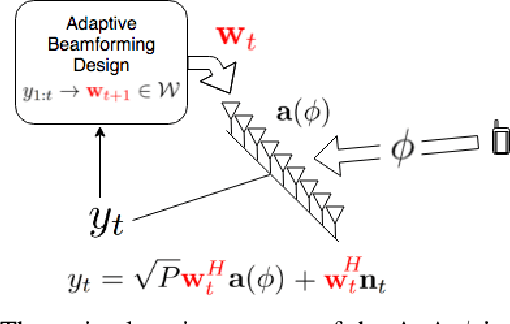
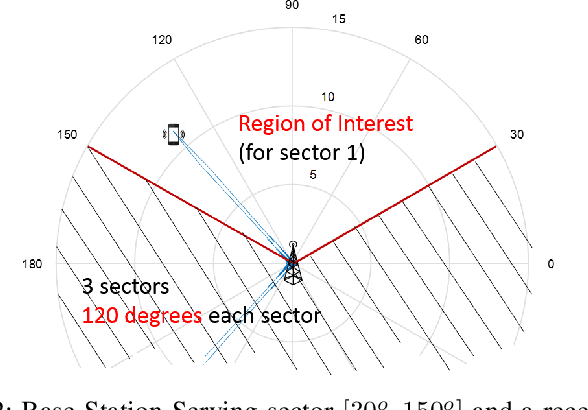
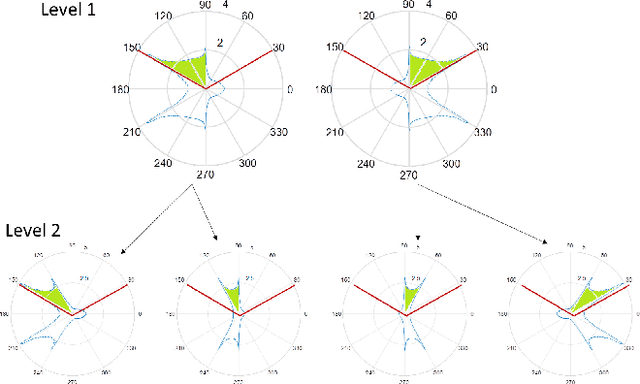
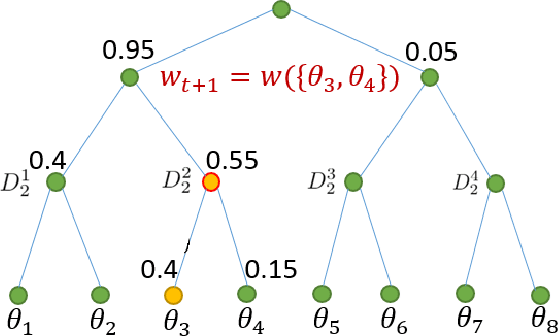
Active Learning and CSI acquisition for mmWave Initial Alignment

Millimeter wave (mmWave) communication with large antenna arrays is a promising technique to enable extremely high data rates due to large available bandwidth. Given the knowledge of an optimal directional beamforming vector, large antenna arrays have been shown to overcome both the severe signal attenuation in mmWave. However, fundamental limits and achievable learning of an optimal beamforming vector remain. This paper considers the problem of adaptive and sequential optimization of the beamforming vectors during the initial access phase of communication. With a single-path channel model, the problem is reduced to actively learning the Angle-of-Arrival (AoA) of the signal sent from the user to the Base Station (BS). Drawing on the recent results in the design of a hierarchical beamforming codebook [1], sequential measurement dependent noisy search [2], and active learning from an imperfect labeler [3], an adaptive and sequential alignment algorithm is proposed. For any given resolution and error probability of the estimated AoA, an upper bound on the expected search time of the proposed algorithm is derived via the Extrinsic Jensen Shannon Divergence. The upper bound demonstrates that the search time of the proposed algorithm asymptotically matches the performance of the noiseless bisection search up to a constant factor characterizing the AoA acquisition rate. Furthermore, the acquired AoA error probability decays exponentially fast with the search time with an exponent that is a decreasing function of the acquisition rate.Numerically, the proposed algorithm is compared with prior work where a significant improvement of the system communication rate is observed. Most notably, in the relevant regime of low (- 10dB to 5dB) raw SNR, this establishes the first practically viable solution for initial access and, hence, the first demonstration of stand-alone mmWave communication.