When to Preempt in a Status Update System?

We consider a time slotted status update system with an error-free preemptive queue. The goal of the sampler-scheduler pair is to minimize the age of information at the monitor by sampling and transmitting the freshly sampled update packets to the monitor. The sampler-scheduler pair also has a choice to preempt an old update packet from the server and transmit a new update packet to the server. We formulate this problem as a Markov decision process and find the optimal sampling policy. We show that it is optimal for the sampler-scheduler pair to sample a new packet immediately upon the reception of an update packet at the monitor. We also show that the optimal choice for the scheduler is to preempt an update packet in the server, if the age of that packet crosses a fixed threshold. Finally, we find the optimal preemption threshold when the range of the service time of the server is finite, otherwise we find the $\epsilon$-optimal preemption threshold.

Age-Based Cache Updating Under Timestomping

We consider a slotted communication system consisting of a source, a cache, a user and a timestomping adversary. The time horizon consists of total $T$ time slots, such that the source transmits update packets to the user directly over $T_{1}$ time slots and to the cache over $T_{2}$ time slots. We consider $T_{1}\ll T_{2}$, $T_{1}+T_{2} < T$, such that the source transmits to the user once between two consecutive cache updates. Update packets are marked with timestamps corresponding to their generation times at the source. All nodes have a buffer size of one and store the packet with the latest timestamp to minimize their age of information. In this setting, we consider the presence of an oblivious adversary that fully controls the communication link between the cache and the user. The adversary manipulates the timestamps of outgoing packets from the cache to the user, with the goal of bringing staleness at the user node. At each time slot, the adversary can choose to either forward the cached packet to the user, after changing its timestamp to current time $t$, thereby rebranding an old packet as a fresh packet and misleading the user into accepting it, or stay idle. The user compares the timestamps of every received packet with the latest packet in its possession to keep the fresher one and discard the staler packet. If the user receives update packets from both cache and source in a time slot, then the packet from source prevails. The goal of the source is to design an algorithm to minimize the average age at the user, and the goal of the adversary is to increase the average age at the user. We formulate this problem in an online learning setting and provide a fundamental lower bound on the competitive ratio for this problem. We further propose a deterministic algorithm with a provable guarantee on its competitive ratio.

To Re-transmit or Not to Re-transmit for Freshness

We consider a time slotted communication network with a base station (BS) and a user. At each time slot a fresh update packet arrives at the BS with probability $p>0$. When the BS transmits an update packet for the first time, it goes through with a success probability of $q_1$. In all subsequent re-transmissions, the packet goes through with a success probability of $q_2$ where $q_2>q_1$, due to the accumulation of observations at the receiver used to decode the packet. When the packet goes through the first time, the age of the user drops to 1, while when the packet goes through in subsequent transmissions, the age of the user drops to the age of the packet since its generation. Thus, when the BS is in the process of re-transmitting an old packet, if it receives a new packet, it has to decide whether to re-transmit the old packet with higher probability of successful transmission but resulting in higher age, or to transmit the new packet which will result in a lower age upon successful reception but this will happen with lower probability. In this paper, we provide an optimal algorithm to solve this problem.

The Freshness Game: Timely Communications in the Presence of an Adversary

We consider a communication system where a base station (BS) transmits update packets to $N$ users, one user at a time, over a wireless channel. We investigate the age of this status updating system with an adversary that jams the update packets in the downlink. We consider two system models: with diversity and without diversity. In the model without diversity, we show that if the BS schedules the users with a stationary randomized policy, then the optimal choice for the adversary is to block the user which has the lowest probability of getting scheduled by the BS, at the middle of the time horizon, consecutively for $\alpha T$ time slots. In the model with diversity, we show that for large $T$, the uniform user scheduling algorithm together with the uniform sub-carrier choosing algorithm is $\frac{2 N_{sub}}{N_{sub}-1}$ optimal. Next, we investigate the game theoretic equilibrium points of this status updating system. For the model without diversity, we show that a Nash equilibrium does not exist, however, a Stackelberg equilibrium exists when the scheduling algorithm of the BS acts as the leader and the adversary acts as the follower. For the model with diversity, we show that a Nash equilibrium exists and identify the Nash equilibrium. Finally, we extend the model without diversity to the case where the BS can serve multiple users and the adversary can jam multiple users, at a time.

Minimizing the Age of Information Over an Erasure Channel for Random Packet Arrivals With a Storage Option at the Transmitter

We consider a time slotted communication system consisting of a base station (BS) and a user. At each time slot an update packet arrives at the BS with probability $p$, and the BS successfully transmits the update packet with probability $q$ over an erasure channel. We assume that the BS has a unit size buffer where it can store an update packet upon paying a storage cost $c$. There is a trade-off between the age of information and the storage cost. We formulate this trade-off as a Markov decision process and find an optimal switching type storage policy.

Age of Information of a Power Constrained Scheduler in the Presence of a Power Constrained Adversary

We consider a time slotted communication network consisting of a base station (BS), an adversary, $N$ users and $N_s$ communication channels. Both the BS and the adversary have average power constraints and the probability of successful transmission of an update packet depends on the transmission power of the BS and the blocking power of the adversary. We provide a universal lower bound for the average age for this communication network. We prove that the uniform scheduling algorithm with any feasible transmission power choosing policy is $4$ optimal; and the max-age user choosing policy is $2$ optimal. In the second part of the paper, we consider the setting where the BS chooses a transmission policy and the adversary chooses a blocking policy from the set of randomized stationary policies. We show that the Nash equilibrium point may or may not exist for this communication network. We find special cases where the Nash equilibrium always exists.

Game Theoretic Analysis of an Adversarial Status Updating System

We investigate the game theoretic equilibrium points of a status updating system with an adversary that jams the updates in the downlink. We consider the system models with and without diversity. The adversary can jam up to $\alpha$ proportion of the entire communication window. In the model without diversity, in each time slot, the base station schedules a user from $N$ users according to a stationary distribution. The adversary blocks (jams) $\alpha T$ time slots of its choosing out of the total $T$ time slots. For this system, we show that a Nash equilibrium does not exist, however, a Stackelberg equilibrium exists when the scheduling algorithm of the base station acts as the leader and the adversary acts as the follower. In the model with diversity, in each time slot, the base station schedules a user from $N$ users and chooses a sub-carrier from $N_{sub}$ sub-carriers to transmit update packets to the scheduled user according to a stationary distribution. The adversary blocks $\alpha T$ time slots of its choosing out of $T$ time slots at the sub-carriers of its choosing. For this system, we show that a Nash equilibrium exists and identify the Nash equilibrium.

Age of Information in the Presence of an Adversary

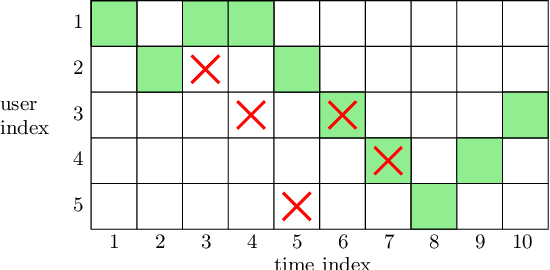
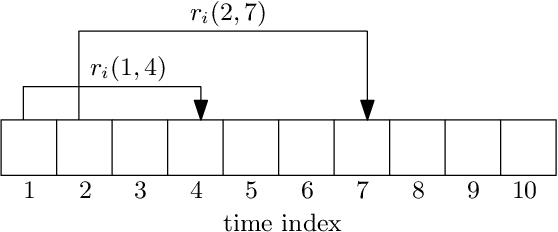
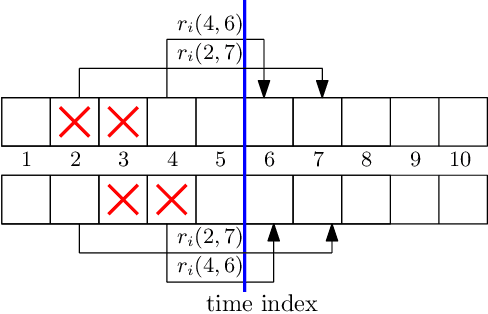
We consider a communication system where a base station serves $N$ users, one user at a time, over a wireless channel. We consider the timeliness of the communication of each user via the age of information metric. A constrained adversary can block at most a given fraction, $\alpha$, of the time slots over a horizon of $T$ slots, i.e., it can block at most $\alpha T$ slots. We show that an optimum adversary blocks $\alpha T$ consecutive time slots of a randomly selected user. The interesting consecutive property of the blocked time slots is due to the cumulative nature of the age metric.