Age of Information in the Presence of an Adversary
Paper and Code
Feb 08, 2022
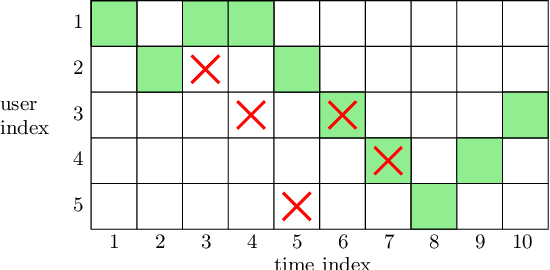
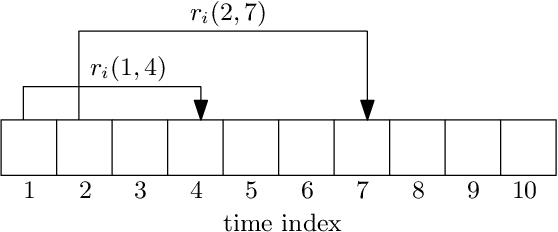
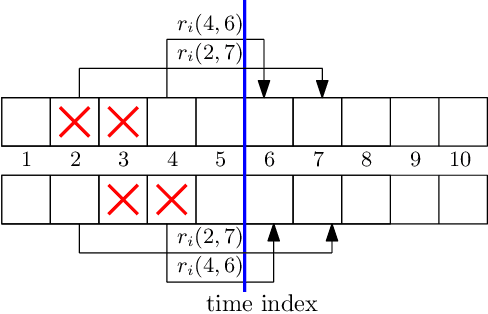
We consider a communication system where a base station serves $N$ users, one user at a time, over a wireless channel. We consider the timeliness of the communication of each user via the age of information metric. A constrained adversary can block at most a given fraction, $\alpha$, of the time slots over a horizon of $T$ slots, i.e., it can block at most $\alpha T$ slots. We show that an optimum adversary blocks $\alpha T$ consecutive time slots of a randomly selected user. The interesting consecutive property of the blocked time slots is due to the cumulative nature of the age metric.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge