Sparse but Strong: Crafting Adversarially Robust Graph Lottery Tickets

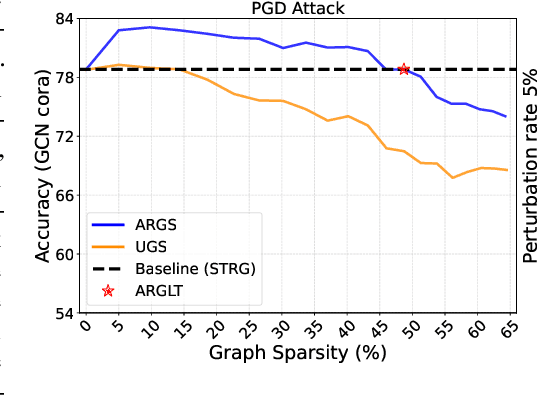
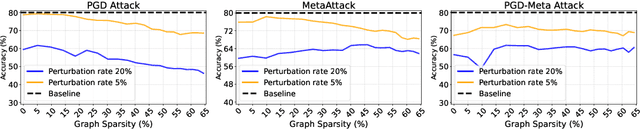
Graph Lottery Tickets (GLTs), comprising a sparse adjacency matrix and a sparse graph neural network (GNN), can significantly reduce the inference latency and compute footprint compared to their dense counterparts. Despite these benefits, their performance against adversarial structure perturbations remains to be fully explored. In this work, we first investigate the resilience of GLTs against different structure perturbation attacks and observe that they are highly vulnerable and show a large drop in classification accuracy. Based on this observation, we then present an adversarially robust graph sparsification (ARGS) framework that prunes the adjacency matrix and the GNN weights by optimizing a novel loss function capturing the graph homophily property and information associated with both the true labels of the train nodes and the pseudo labels of the test nodes. By iteratively applying ARGS to prune both the perturbed graph adjacency matrix and the GNN model weights, we can find adversarially robust graph lottery tickets that are highly sparse yet achieve competitive performance under different untargeted training-time structure attacks. Evaluations conducted on various benchmarks, considering different poisoning structure attacks, namely, PGD, MetaAttack, Meta-PGD, and PR-BCD demonstrate that the GLTs generated by ARGS can significantly improve the robustness, even when subjected to high levels of sparsity.

ReIGNN: State Register Identification Using Graph Neural Networks for Circuit Reverse Engineering

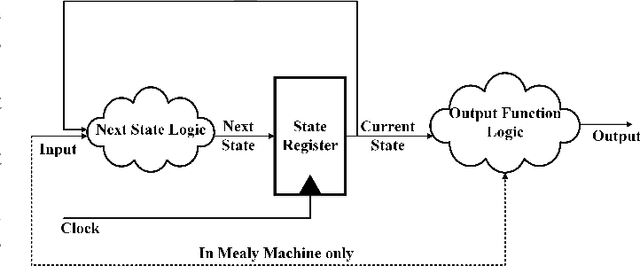
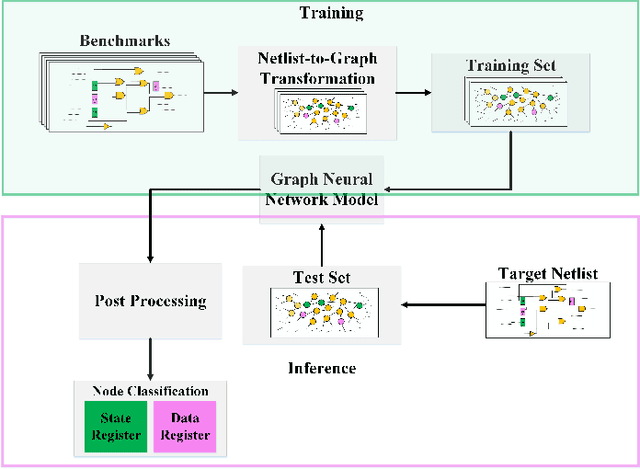
Reverse engineering an integrated circuit netlist is a powerful tool to help detect malicious logic and counteract design piracy. A critical challenge in this domain is the correct classification of data-path and control-logic registers in a design. We present ReIGNN, a novel learning-based register classification methodology that combines graph neural networks (GNNs) with structural analysis to classify the registers in a circuit with high accuracy and generalize well across different designs. GNNs are particularly effective in processing circuit netlists in terms of graphs and leveraging properties of the nodes and their neighborhoods to learn to efficiently discriminate between different types of nodes. Structural analysis can further rectify any registers misclassified as state registers by the GNN by analyzing strongly connected components in the netlist graph. Numerical results on a set of benchmarks show that ReIGNN can achieve, on average, 96.5% balanced accuracy and 97.7% sensitivity across different designs.