InfoGram and Admissible Machine Learning

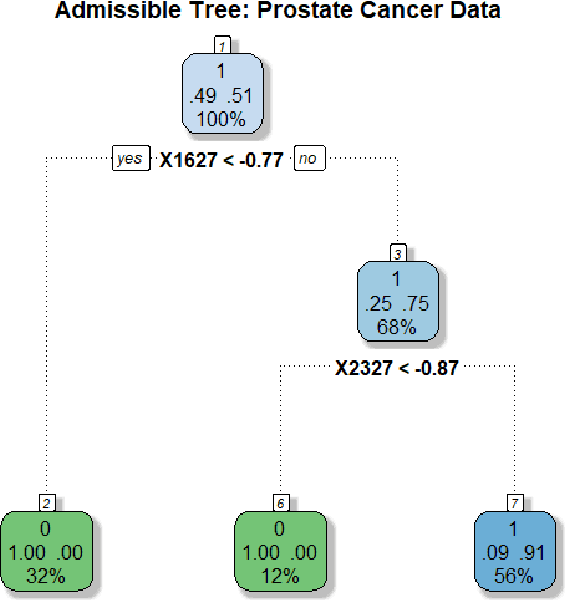
We have entered a new era of machine learning (ML), where the most accurate algorithm with superior predictive power may not even be deployable, unless it is admissible under the regulatory constraints. This has led to great interest in developing fair, transparent and trustworthy ML methods. The purpose of this article is to introduce a new information-theoretic learning framework (admissible machine learning) and algorithmic risk-management tools (InfoGram, L-features, ALFA-testing) that can guide an analyst to redesign off-the-shelf ML methods to be regulatory compliant, while maintaining good prediction accuracy. We have illustrated our approach using several real-data examples from financial sectors, biomedical research, marketing campaigns, and the criminal justice system.

On The Problem of Relevance in Statistical Inference

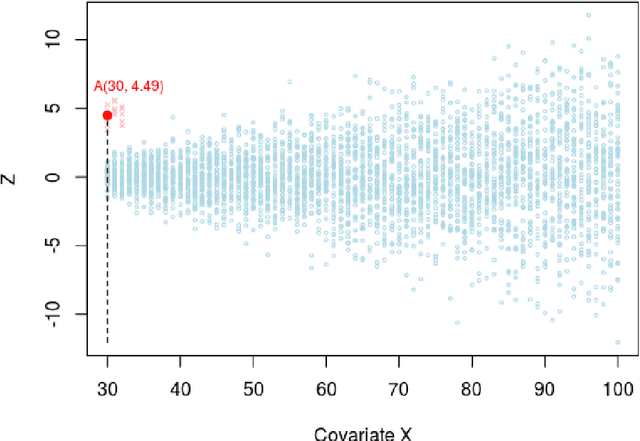
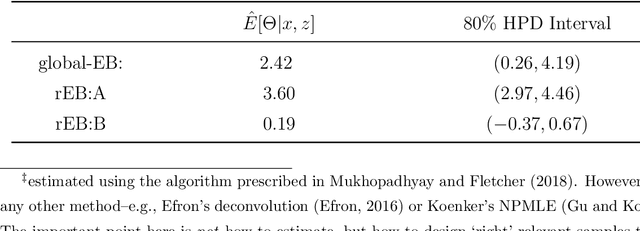
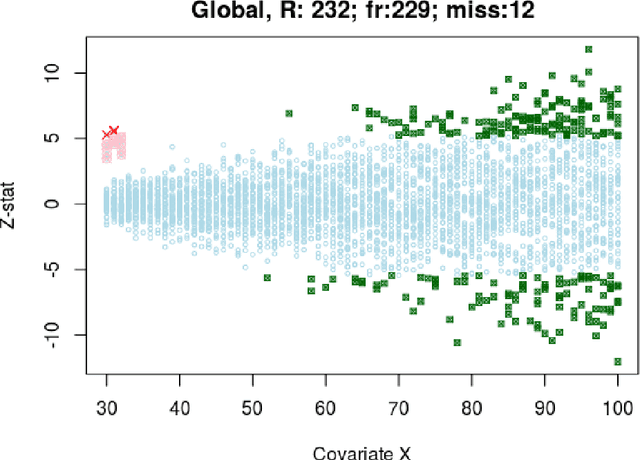
How many statistical inference tools we have for inference from massive data? A huge number, but only when we are ready to assume the given database is homogenous, consisting of a large cohort of "similar" cases. Why we need the homogeneity assumption? To make `learning from the experience of others' or `borrowing strength' possible. But, what if, we are dealing with a massive database of heterogeneous cases (which is a norm in almost all modern data-science applications including neuroscience, genomics, healthcare, and astronomy)? How many methods we have in this situation? Not much, if not ZERO. Why? It's not obvious how to go about gathering strength when each piece of information is fuzzy. The danger is that, if we include irrelevant cases, borrowing information might heavily damage the quality of the inference! This raises some fundamental questions for big data inference: When (not) to borrow? Whom (not) to borrow? How (not) to borrow? These questions are at the heart of the "Problem of Relevance" in statistical inference -- a puzzle that has remained too little addressed since its inception nearly half a century ago. Here we offer the first practical theory of relevance with precisely describable statistical formulation and algorithm. Through examples, we demonstrate how our new statistical perspective answers previously unanswerable questions in a realistic and feasible way.

Nonlinear Time Series Modeling: A Unified Perspective, Algorithm, and Application

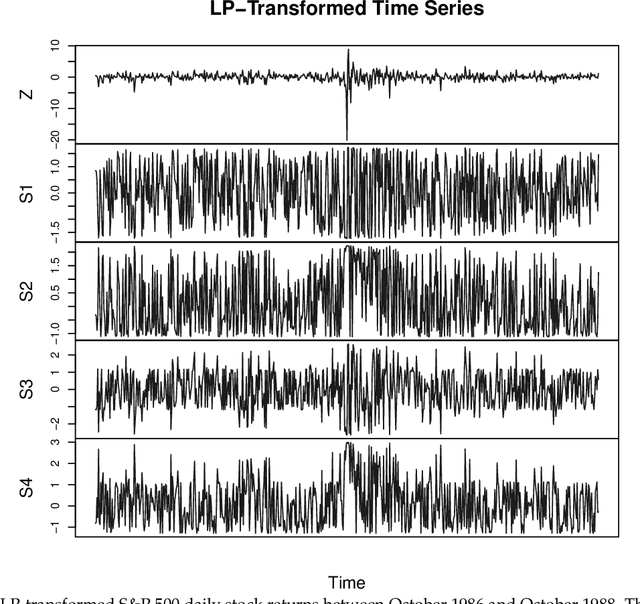
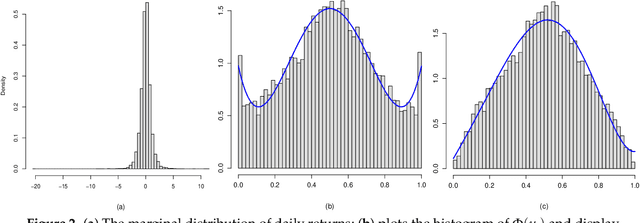
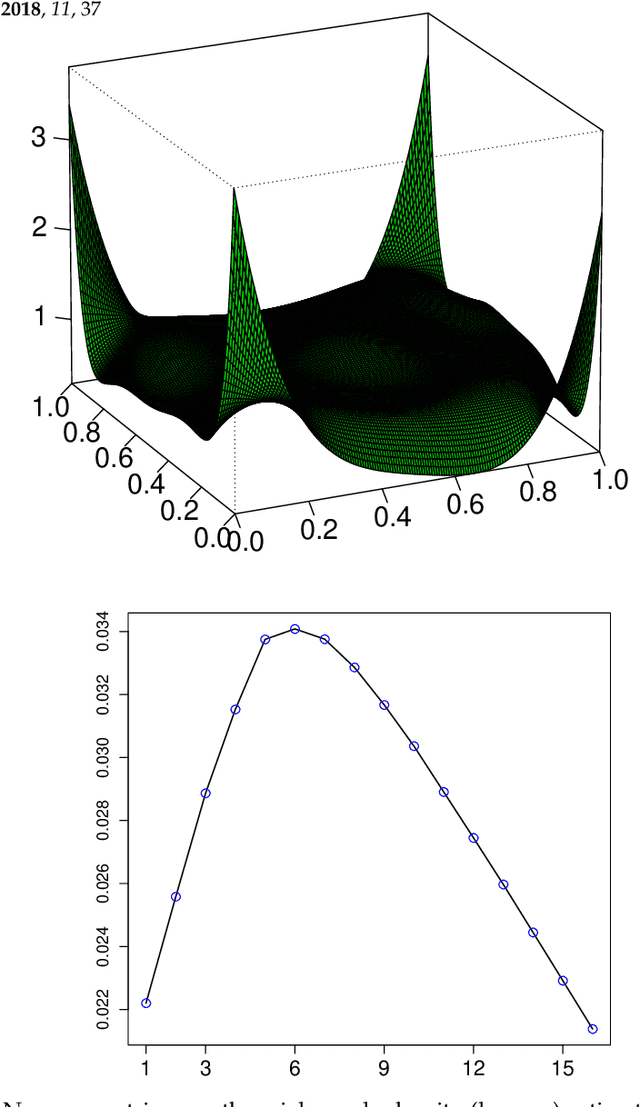
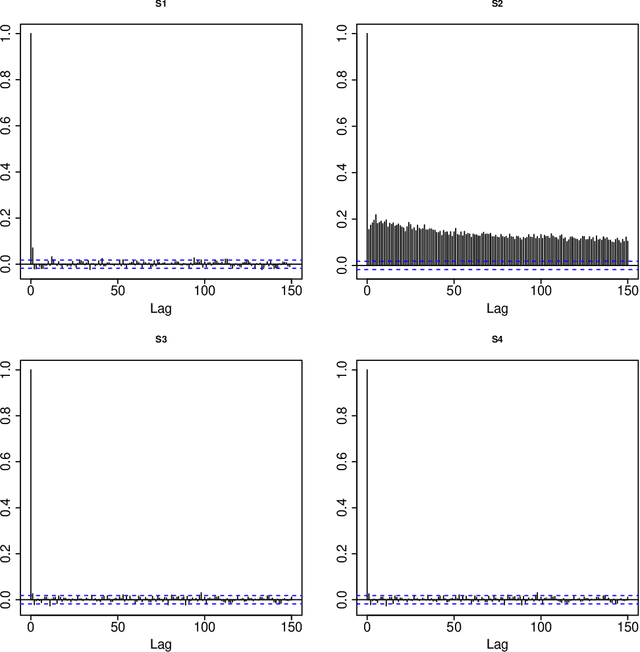
A new comprehensive approach to nonlinear time series analysis and modeling is developed in the present paper. We introduce novel data-specific mid-distribution based Legendre Polynomial (LP) like nonlinear transformations of the original time series Y(t) that enables us to adapt all the existing stationary linear Gaussian time series modeling strategy and made it applicable for non-Gaussian and nonlinear processes in a robust fashion. The emphasis of the present paper is on empirical time series modeling via the algorithm LPTime. We demonstrate the effectiveness of our theoretical framework using daily S&P 500 return data between Jan/2/1963 - Dec/31/2009. Our proposed LPTime algorithm systematically discovers all the `stylized facts' of the financial time series automatically all at once, which were previously noted by many researchers one at a time.

Unified Statistical Theory of Spectral Graph Analysis

The goal of this paper is to show that there exists a simple, yet universal statistical logic of spectral graph analysis by recasting it into a nonparametric function estimation problem. The prescribed viewpoint appears to be good enough to accommodate most of the existing spectral graph techniques as a consequence of just one single formalism and algorithm.

CDfdr: A Comparison Density Approach to Local False Discovery Rate Estimation

Efron et al. (2001) proposed empirical Bayes formulation of the frequentist Benjamini and Hochbergs False Discovery Rate method (Benjamini and Hochberg,1995). This article attempts to unify the `two cultures' using concepts of comparison density and distribution function. We have also shown how almost all of the existing local fdr methods can be viewed as proposing various model specification for comparison density - unifies the vast literature of false discovery methods under one concept and notation.

United Statistical Algorithm, Small and Big Data: Future OF Statistician

This article provides the role of big idea statisticians in future of Big Data Science. We describe the `United Statistical Algorithms' framework for comprehensive unification of traditional and novel statistical methods for modeling Small Data and Big Data, especially mixed data (discrete, continuous).

Modeling, dependence, classification, united statistical science, many cultures

Breiman (2001) proposed to statisticians awareness of two cultures: 1. Parametric modeling culture, pioneered by R.A.Fisher and Jerzy Neyman; 2. Algorithmic predictive culture, pioneered by machine learning research. Parzen (2001), as a part of discussing Breiman (2001), proposed that researchers be aware of many cultures, including the focus of our research: 3. Nonparametric, quantile based, information theoretic modeling. We provide a unification of many statistical methods for traditional small data sets and emerging big data sets in terms of comparison density, copula density, measure of dependence, correlation, information, new measures (called LP score comoments) that apply to long tailed distributions with out finite second order moments. A very important goal is to unify methods for discrete and continuous random variables. Our research extends these methods to modern high dimensional data modeling.