Nonlinear Time Series Modeling: A Unified Perspective, Algorithm, and Application

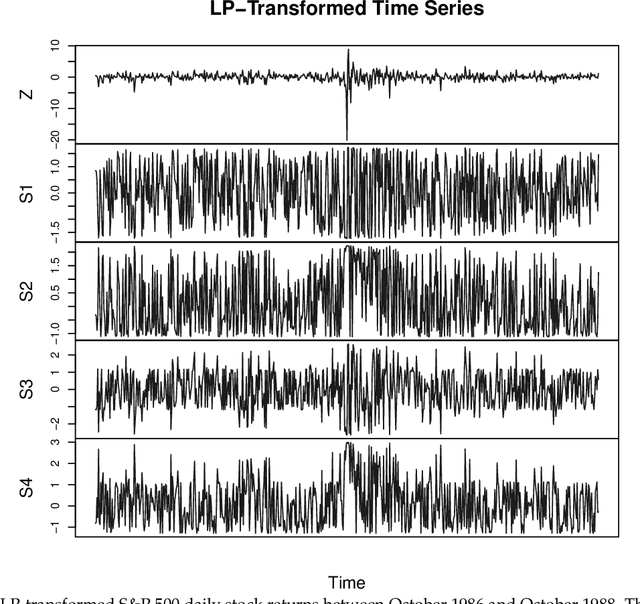
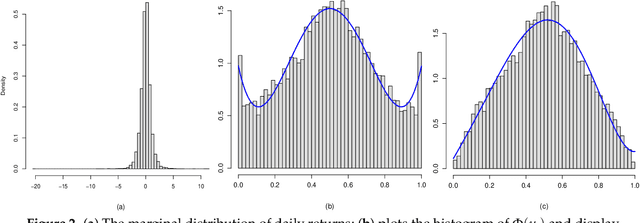
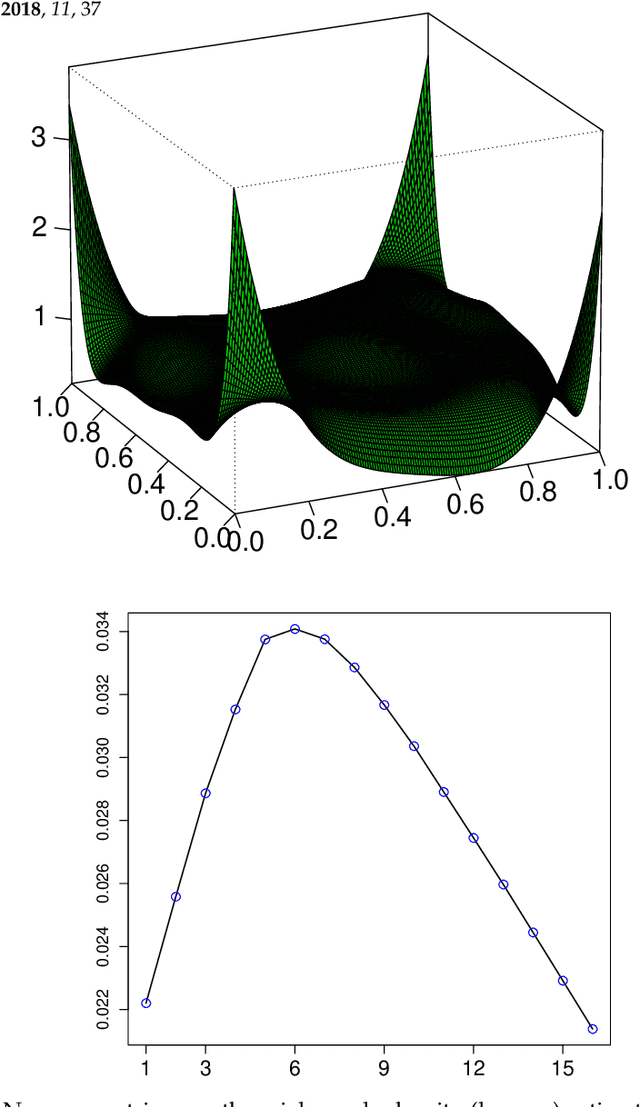
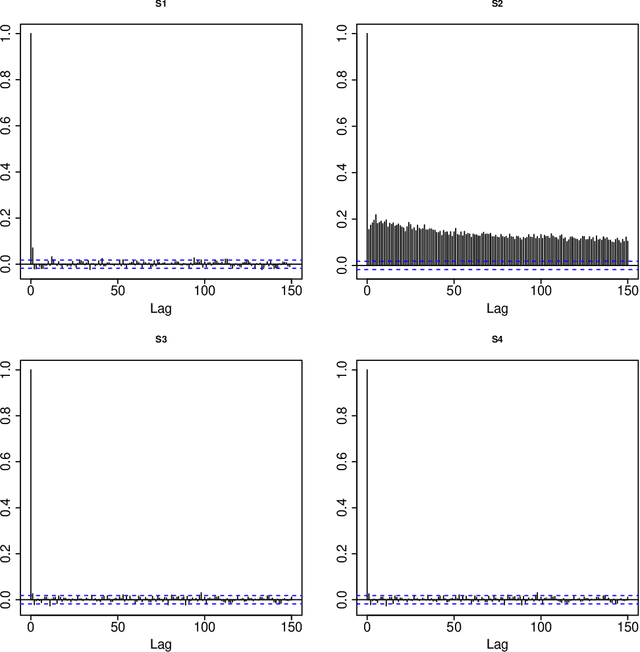
A new comprehensive approach to nonlinear time series analysis and modeling is developed in the present paper. We introduce novel data-specific mid-distribution based Legendre Polynomial (LP) like nonlinear transformations of the original time series Y(t) that enables us to adapt all the existing stationary linear Gaussian time series modeling strategy and made it applicable for non-Gaussian and nonlinear processes in a robust fashion. The emphasis of the present paper is on empirical time series modeling via the algorithm LPTime. We demonstrate the effectiveness of our theoretical framework using daily S&P 500 return data between Jan/2/1963 - Dec/31/2009. Our proposed LPTime algorithm systematically discovers all the `stylized facts' of the financial time series automatically all at once, which were previously noted by many researchers one at a time.

United Statistical Algorithm, Small and Big Data: Future OF Statistician

This article provides the role of big idea statisticians in future of Big Data Science. We describe the `United Statistical Algorithms' framework for comprehensive unification of traditional and novel statistical methods for modeling Small Data and Big Data, especially mixed data (discrete, continuous).

Modeling, dependence, classification, united statistical science, many cultures

Breiman (2001) proposed to statisticians awareness of two cultures: 1. Parametric modeling culture, pioneered by R.A.Fisher and Jerzy Neyman; 2. Algorithmic predictive culture, pioneered by machine learning research. Parzen (2001), as a part of discussing Breiman (2001), proposed that researchers be aware of many cultures, including the focus of our research: 3. Nonparametric, quantile based, information theoretic modeling. We provide a unification of many statistical methods for traditional small data sets and emerging big data sets in terms of comparison density, copula density, measure of dependence, correlation, information, new measures (called LP score comoments) that apply to long tailed distributions with out finite second order moments. A very important goal is to unify methods for discrete and continuous random variables. Our research extends these methods to modern high dimensional data modeling.