On The Problem of Relevance in Statistical Inference

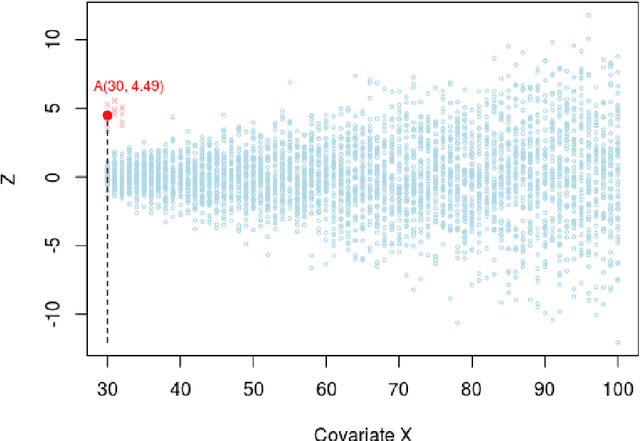
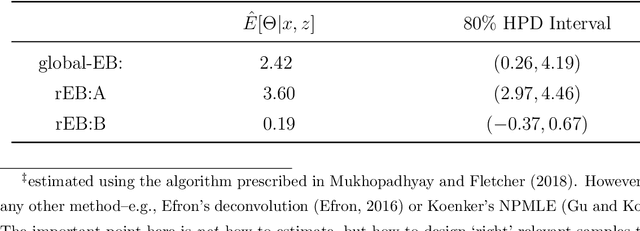
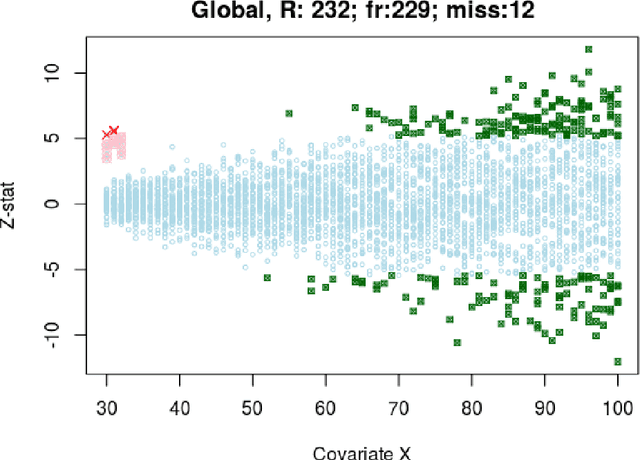
How many statistical inference tools we have for inference from massive data? A huge number, but only when we are ready to assume the given database is homogenous, consisting of a large cohort of "similar" cases. Why we need the homogeneity assumption? To make `learning from the experience of others' or `borrowing strength' possible. But, what if, we are dealing with a massive database of heterogeneous cases (which is a norm in almost all modern data-science applications including neuroscience, genomics, healthcare, and astronomy)? How many methods we have in this situation? Not much, if not ZERO. Why? It's not obvious how to go about gathering strength when each piece of information is fuzzy. The danger is that, if we include irrelevant cases, borrowing information might heavily damage the quality of the inference! This raises some fundamental questions for big data inference: When (not) to borrow? Whom (not) to borrow? How (not) to borrow? These questions are at the heart of the "Problem of Relevance" in statistical inference -- a puzzle that has remained too little addressed since its inception nearly half a century ago. Here we offer the first practical theory of relevance with precisely describable statistical formulation and algorithm. Through examples, we demonstrate how our new statistical perspective answers previously unanswerable questions in a realistic and feasible way.