Individuation of 3D perceptual units from neurogeometry of binocular cells

We model the functional architecture of the early stages of three-dimensional vision by extending the neurogeometric sub-Riemannian model for stereo-vision introduced in \cite{BCSZ23}. A new framework for correspondence is introduced that integrates a neural-based algorithm to achieve stereo correspondence locally while, simultaneously, organizing the corresponding points into global perceptual units. The result is an effective scene segmentation. We achieve this using harmonic analysis on the sub-Riemannian structure and show, in a comparison against Riemannian distance, that the sub-Riemannian metric is central to the solution.

A separability-based approach to quantifying generalization: which layer is best?

Generalization to unseen data remains poorly understood for deep learning classification and foundation models. How can one assess the ability of networks to adapt to new or extended versions of their input space in the spirit of few-shot learning, out-of-distribution generalization, and domain adaptation? Which layers of a network are likely to generalize best? We provide a new method for evaluating the capacity of networks to represent a sampled domain, regardless of whether the network has been trained on all classes in the domain. Our approach is the following: after fine-tuning state-of-the-art pre-trained models for visual classification on a particular domain, we assess their performance on data from related but distinct variations in that domain. Generalization power is quantified as a function of the latent embeddings of unseen data from intermediate layers for both unsupervised and supervised settings. Working throughout all stages of the network, we find that (i) high classification accuracy does not imply high generalizability; and (ii) deeper layers in a model do not always generalize the best, which has implications for pruning. Since the trends observed across datasets are largely consistent, we conclude that our approach reveals (a function of) the intrinsic capacity of the different layers of a model to generalize.

Learning dynamic representations of the functional connectome in neurobiological networks

The static synaptic connectivity of neuronal circuits stands in direct contrast to the dynamics of their function. As in changing community interactions, different neurons can participate actively in various combinations to effect behaviors at different times. We introduce an unsupervised approach to learn the dynamic affinities between neurons in live, behaving animals, and to reveal which communities form among neurons at different times. The inference occurs in two major steps. First, pairwise non-linear affinities between neuronal traces from brain-wide calcium activity are organized by non-negative tensor factorization (NTF). Each factor specifies which groups of neurons are most likely interacting for an inferred interval in time, and for which animals. Finally, a generative model that allows for weighted community detection is applied to the functional motifs produced by NTF to reveal a dynamic functional connectome. Since time codes the different experimental variables (e.g., application of chemical stimuli), this provides an atlas of neural motifs active during separate stages of an experiment (e.g., stimulus application or spontaneous behaviors). Results from our analysis are experimentally validated, confirming that our method is able to robustly predict causal interactions between neurons to generate behavior. Code is available at https://github.com/dyballa/dynamic-connectomes.

Zero-shot generalization across architectures for visual classification

Generalization to unseen data is a key desideratum for deep networks, but its relation to classification accuracy is unclear. Using a minimalist vision dataset and a measure of generalizability, we show that popular networks, from deep convolutional networks (CNNs) to transformers, vary in their power to extrapolate to unseen classes both across layers and across architectures. Accuracy is not a good predictor of generalizability, and generalization varies non-monotonically with layer depth. Code is available at https://github.com/dyballa/zero-shot-generalization.

IAN: Iterated Adaptive Neighborhoods for manifold learning and dimensionality estimation

Invoking the manifold assumption in machine learning requires knowledge of the manifold's geometry and dimension, and theory dictates how many samples are required. However, in applications data are limited, sampling may not be uniform, and manifold properties are unknown and (possibly) non-pure; this implies that neighborhoods must adapt to the local structure. We introduce an algorithm for inferring adaptive neighborhoods for data given by a similarity kernel. Starting with a locally-conservative neighborhood (Gabriel) graph, we sparsify it iteratively according to a weighted counterpart. In each step, a linear program yields minimal neighborhoods globally and a volumetric statistic reveals neighbor outliers likely to violate manifold geometry. We apply our adaptive neighborhoods to non-linear dimensionality reduction, geodesic computation and dimension estimation. A comparison against standard algorithms using, e.g., k-nearest neighbors, demonstrates their usefulness.

From Boundaries to Bumps: when closed contours are critical

Invariants underlying shape inference are elusive: a variety of shapes can give rise to the same image, and a variety of images can be rendered from the same shape. The occluding contour is a rare exception: it has both image salience, in terms of isophotes, and surface meaning, in terms of surface normal. We relax the notion of occluding contour to define closed extremal curves, a new shape invariant that exists at the topological level. They surround bumps, a common but ill-specified interior shape component, and formalize the qualitative nature of bump perception. Extremal curves are biologically computable, unify shape inferences from shading, texture, and specular materials, and predict new phenomena in bump perception.

Tensors, Differential Geometry and Statistical Shading Analysis

We develop a linear algebraic framework for the shape-from-shading problem, because tensors arise when scalar (e.g. image) and vector (e.g. surface normal) fields are differentiated multiple times. Using this framework, we first investigate when image derivatives exhibit invariance to changing illumination by calculating the statistics of image derivatives under general distributions on the light source. Second, we apply that framework to develop Taylor-like expansions, and build a boot-strapping algorithm to find the polynomial surface solutions (under any light source) consistent with a given patch to arbitrary order. A generic constraint on the light source restricts these solutions to a 2-D subspace, plus an unknown rotation matrix. It is this unknown matrix that encapsulates the ambiguity in the problem. Finally, we use the framework to computationally validate the hypothesis that image orientations (derivatives) provide increased invariance to illumination by showing (for a Lambertian model) that a shape-from-shading algorithm matching gradients instead of intensities provides more accurate reconstructions when illumination is incorrectly estimated under a flatness prior.

Critical Contours: An Invariant Linking Image Flow with Salient Surface Organization

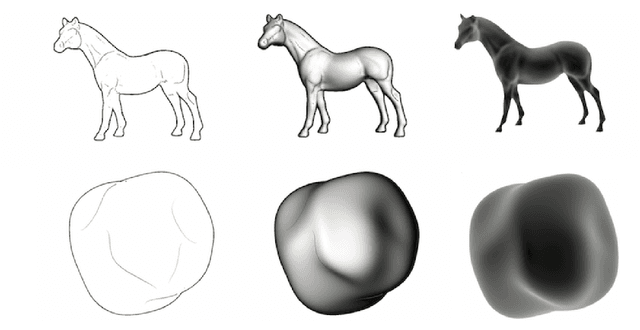
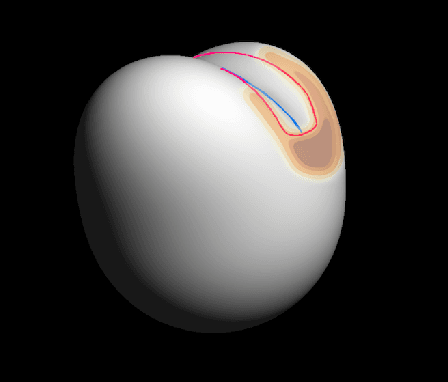
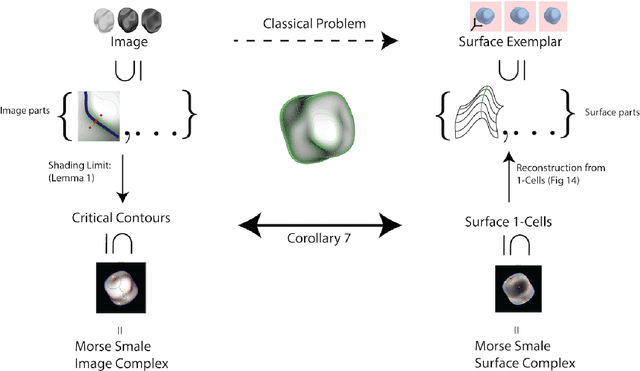
We exploit a key result from visual psychophysics---that individuals perceive shape qualitatively---to develop the use of a geometrical/topological "invariant'' (the Morse--Smale complex) relating image structure with surface structure. Differences across individuals are minimal near certain configurations such as ridges and boundaries, and it is these configurations that are often represented in line drawings. In particular, we introduce a method for inferring a qualitative three-dimensional shape from shading patterns that link the shape-from-shading inference with shape-from-contour inference. For a given shape, certain shading patches approach "line drawings'' in a well-defined limit. Under this limit, and invariably with respect to rendering choices, these shading patterns provide a qualitative description of the surface. We further show that, under this model, the contours partition the surface into meaningful parts using the Morse--Smale complex. These critical contours are the (perceptually) stable parts of this complex and are invariant over a wide class of rendering models. Intuitively, our main result shows that critical contours partition smooth surfaces into bumps and valleys, in effect providing a scaffold on the image from which a full surface can be interpolated.

Feature Selection Facilitates Learning Mixtures of Discrete Product Distributions

Feature selection can facilitate the learning of mixtures of discrete random variables as they arise, e.g. in crowdsourcing tasks. Intuitively, not all workers are equally reliable but, if the less reliable ones could be eliminated, then learning should be more robust. By analogy with Gaussian mixture models, we seek a low-order statistical approach, and here introduce an algorithm based on the (pairwise) mutual information. This induces an order over workers that is well structured for the `one coin' model. More generally, it is justified by a goodness-of-fit measure and is validated empirically. Improvement in real data sets can be substantial.

What's In A Patch, I: Tensors, Differential Geometry and Statistical Shading Analysis

We develop a linear algebraic framework for the shape-from-shading problem, because tensors arise when scalar (e.g. image) and vector (e.g. surface normal) fields are differentiated multiple times. The work is in two parts. In this first part we investigate when image derivatives exhibit invariance to changing illumination by calculating the statistics of image derivatives under general distributions on the light source. We computationally validate the hypothesis that image orientations (derivatives) provide increased invariance to illumination by showing (for a Lambertian model) that a shape-from-shading algorithm matching gradients instead of intensities provides more accurate reconstructions when illumination is incorrectly estimated under a flatness prior.