Tensors, Differential Geometry and Statistical Shading Analysis

We develop a linear algebraic framework for the shape-from-shading problem, because tensors arise when scalar (e.g. image) and vector (e.g. surface normal) fields are differentiated multiple times. Using this framework, we first investigate when image derivatives exhibit invariance to changing illumination by calculating the statistics of image derivatives under general distributions on the light source. Second, we apply that framework to develop Taylor-like expansions, and build a boot-strapping algorithm to find the polynomial surface solutions (under any light source) consistent with a given patch to arbitrary order. A generic constraint on the light source restricts these solutions to a 2-D subspace, plus an unknown rotation matrix. It is this unknown matrix that encapsulates the ambiguity in the problem. Finally, we use the framework to computationally validate the hypothesis that image orientations (derivatives) provide increased invariance to illumination by showing (for a Lambertian model) that a shape-from-shading algorithm matching gradients instead of intensities provides more accurate reconstructions when illumination is incorrectly estimated under a flatness prior.

Critical Contours: An Invariant Linking Image Flow with Salient Surface Organization

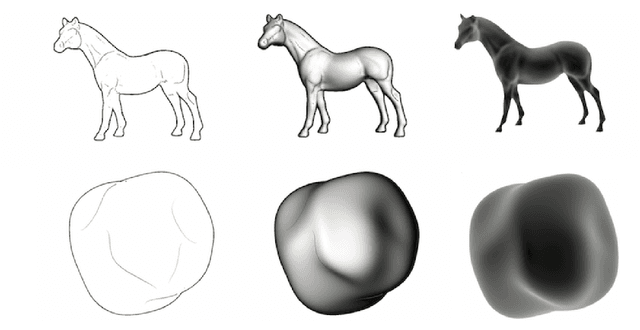
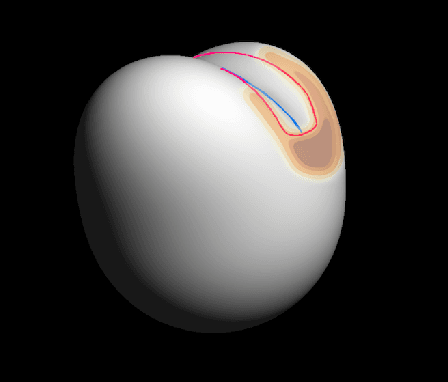
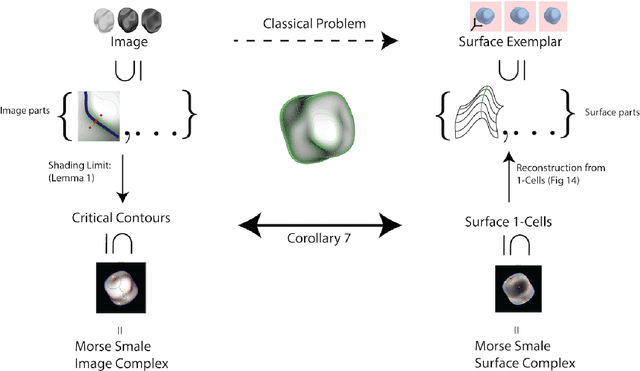
We exploit a key result from visual psychophysics---that individuals perceive shape qualitatively---to develop the use of a geometrical/topological "invariant'' (the Morse--Smale complex) relating image structure with surface structure. Differences across individuals are minimal near certain configurations such as ridges and boundaries, and it is these configurations that are often represented in line drawings. In particular, we introduce a method for inferring a qualitative three-dimensional shape from shading patterns that link the shape-from-shading inference with shape-from-contour inference. For a given shape, certain shading patches approach "line drawings'' in a well-defined limit. Under this limit, and invariably with respect to rendering choices, these shading patterns provide a qualitative description of the surface. We further show that, under this model, the contours partition the surface into meaningful parts using the Morse--Smale complex. These critical contours are the (perceptually) stable parts of this complex and are invariant over a wide class of rendering models. Intuitively, our main result shows that critical contours partition smooth surfaces into bumps and valleys, in effect providing a scaffold on the image from which a full surface can be interpolated.

What's In A Patch, I: Tensors, Differential Geometry and Statistical Shading Analysis

We develop a linear algebraic framework for the shape-from-shading problem, because tensors arise when scalar (e.g. image) and vector (e.g. surface normal) fields are differentiated multiple times. The work is in two parts. In this first part we investigate when image derivatives exhibit invariance to changing illumination by calculating the statistics of image derivatives under general distributions on the light source. We computationally validate the hypothesis that image orientations (derivatives) provide increased invariance to illumination by showing (for a Lambertian model) that a shape-from-shading algorithm matching gradients instead of intensities provides more accurate reconstructions when illumination is incorrectly estimated under a flatness prior.