Critical Contours: An Invariant Linking Image Flow with Salient Surface Organization
Paper and Code
Jul 26, 2018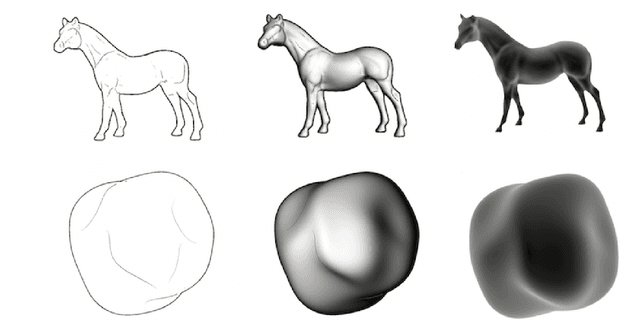

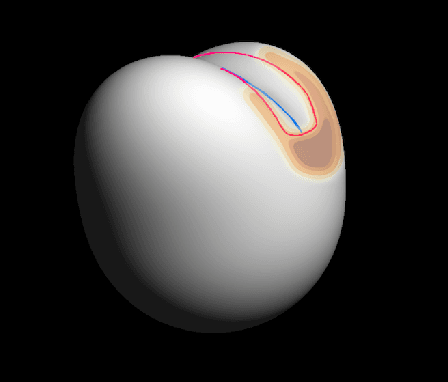
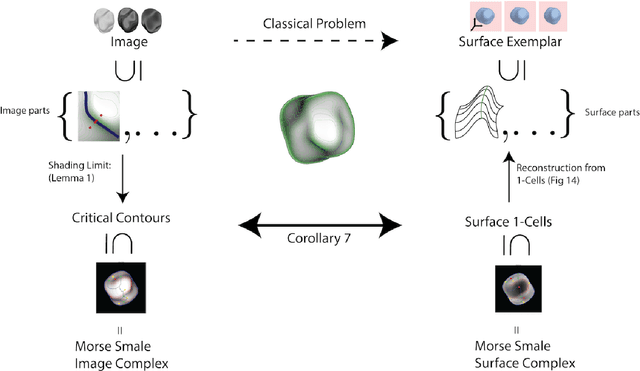
We exploit a key result from visual psychophysics---that individuals perceive shape qualitatively---to develop the use of a geometrical/topological "invariant'' (the Morse--Smale complex) relating image structure with surface structure. Differences across individuals are minimal near certain configurations such as ridges and boundaries, and it is these configurations that are often represented in line drawings. In particular, we introduce a method for inferring a qualitative three-dimensional shape from shading patterns that link the shape-from-shading inference with shape-from-contour inference. For a given shape, certain shading patches approach "line drawings'' in a well-defined limit. Under this limit, and invariably with respect to rendering choices, these shading patterns provide a qualitative description of the surface. We further show that, under this model, the contours partition the surface into meaningful parts using the Morse--Smale complex. These critical contours are the (perceptually) stable parts of this complex and are invariant over a wide class of rendering models. Intuitively, our main result shows that critical contours partition smooth surfaces into bumps and valleys, in effect providing a scaffold on the image from which a full surface can be interpolated.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge