Learning from Irregularly-Sampled Time Series: A Missing Data Perspective

Irregularly-sampled time series occur in many domains including healthcare. They can be challenging to model because they do not naturally yield a fixed-dimensional representation as required by many standard machine learning models. In this paper, we consider irregular sampling from the perspective of missing data. We model observed irregularly-sampled time series data as a sequence of index-value pairs sampled from a continuous but unobserved function. We introduce an encoder-decoder framework for learning from such generic indexed sequences. We propose learning methods for this framework based on variational autoencoders and generative adversarial networks. For continuous irregularly-sampled time series, we introduce continuous convolutional layers that can efficiently interface with existing neural network architectures. Experiments show that our models are able to achieve competitive or better classification results on irregularly-sampled multivariate time series compared to recent RNN models while offering significantly faster training times.

MisGAN: Learning from Incomplete Data with Generative Adversarial Networks

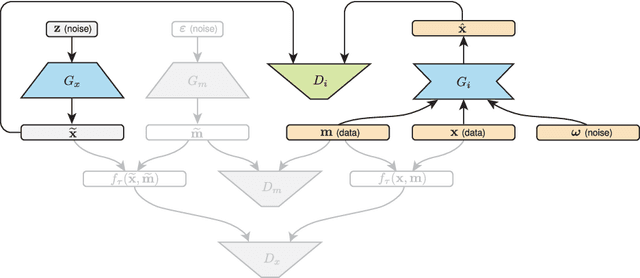
Generative adversarial networks (GANs) have been shown to provide an effective way to model complex distributions and have obtained impressive results on various challenging tasks. However, typical GANs require fully-observed data during training. In this paper, we present a GAN-based framework for learning from complex, high-dimensional incomplete data. The proposed framework learns a complete data generator along with a mask generator that models the missing data distribution. We further demonstrate how to impute missing data by equipping our framework with an adversarially trained imputer. We evaluate the proposed framework using a series of experiments with several types of missing data processes under the missing completely at random assumption.

A scalable end-to-end Gaussian process adapter for irregularly sampled time series classification

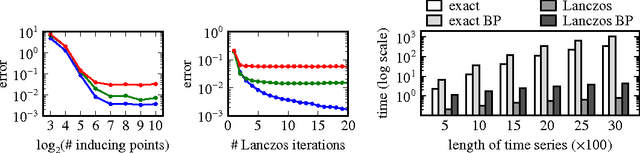
We present a general framework for classification of sparse and irregularly-sampled time series. The properties of such time series can result in substantial uncertainty about the values of the underlying temporal processes, while making the data difficult to deal with using standard classification methods that assume fixed-dimensional feature spaces. To address these challenges, we propose an uncertainty-aware classification framework based on a special computational layer we refer to as the Gaussian process adapter that can connect irregularly sampled time series data to any black-box classifier learnable using gradient descent. We show how to scale up the required computations based on combining the structured kernel interpolation framework and the Lanczos approximation method, and how to discriminatively train the Gaussian process adapter in combination with a number of classifiers end-to-end using backpropagation.