A finite sample analysis of the double descent phenomenon for ridge function estimation

Recent extensive numerical experiments in high scale machine learning have allowed to uncover a quite counterintuitive phase transition, as a function of the ratio between the sample size and the number of parameters in the model. As the number of parameters $p$ approaches the sample size $n$, the generalisation error (a.k.a. testing error) increases, but it many cases, it starts decreasing again past the threshold $p=n$. This surprising phenomenon, brought to the theoretical community attention in \cite{belkin2019reconciling}, has been thorougly investigated lately, more specifically for simpler models than deep neural networks, such as the linear model when the parameter is taken to be the minimum norm solution to the least-square problem, mostly in the asymptotic regime when $p$ and $n$ tend to $+\infty$; see e.g. \cite{hastie2019surprises}. In the present paper, we propose a finite sample analysis of non-linear models of \textit{ridge} type, where we investigate the double descent phenomenon for both the \textit{estimation problem} and the prediction problem. Our results show that the double descent phenomenon can be precisely demonstrated in non-linear settings and complements recent works of \cite{bartlett2020benign} and \cite{chinot2020benign}. Our analysis is based on efficient but elementary tools closely related to the continuous Newton method \cite{neuberger2007continuous}.

Feature selection in weakly coherent matrices

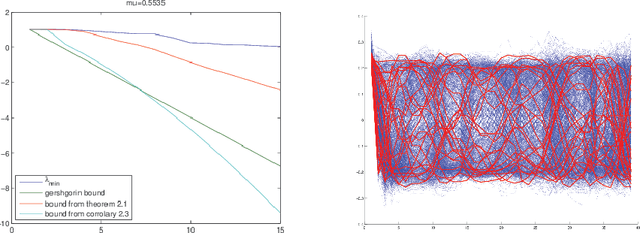
A problem of paramount importance in both pure (Restricted Invertibility problem) and applied mathematics (Feature extraction) is the one of selecting a submatrix of a given matrix, such that this submatrix has its smallest singular value above a specified level. Such problems can be addressed using perturbation analysis. In this paper, we propose a perturbation bound for the smallest singular value of a given matrix after appending a column, under the assumption that its initial coherence is not large, and we use this bound to derive a fast algorithm for feature extraction.

Average performance analysis of the stochastic gradient method for online PCA

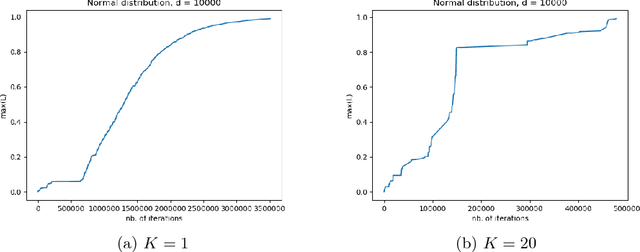
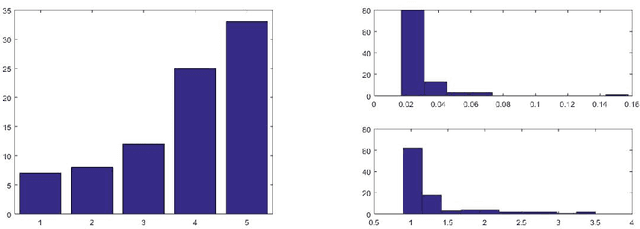
This paper studies the complexity of the stochastic gradient algorithm for PCA when the data are observed in a streaming setting. We also propose an online approach for selecting the learning rate. Simulation experiments confirm the practical relevance of the plain stochastic gradient approach and that drastic improvements can be achieved by learning the learning rate.

Convex recovery of tensors using nuclear norm penalization

The subdifferential of convex functions of the singular spectrum of real matrices has been widely studied in matrix analysis, optimization and automatic control theory. Convex analysis and optimization over spaces of tensors is now gaining much interest due to its potential applications to signal processing, statistics and engineering. The goal of this paper is to present an applications to the problem of low rank tensor recovery based on linear random measurement by extending the results of Tropp to the tensors setting.