Feature selection in weakly coherent matrices
Paper and Code
Apr 03, 2018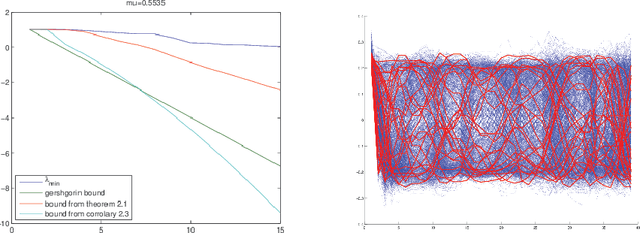

A problem of paramount importance in both pure (Restricted Invertibility problem) and applied mathematics (Feature extraction) is the one of selecting a submatrix of a given matrix, such that this submatrix has its smallest singular value above a specified level. Such problems can be addressed using perturbation analysis. In this paper, we propose a perturbation bound for the smallest singular value of a given matrix after appending a column, under the assumption that its initial coherence is not large, and we use this bound to derive a fast algorithm for feature extraction.
* 14 pages, 6 Figures, Accepted for LVA-ICA 2018 Surrey
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge