Computing Funnels Using Numerical Optimization Based Falsifiers

In this paper, we present an algorithm that computes funnels along trajectories of systems of ordinary differential equations. A funnel is a time-varying set of states containing the given trajectory, for which the evolution from within the set at any given time stays in the funnel. Hence it generalizes the behavior of single trajectories to sets around them, which is an important task, for example, in robot motion planning. In contrast to approaches based on sum-of-squares programming, which poorly scale to high dimensions, our approach is based on falsification and tackles the funnel computation task directly, through numerical optimization. This approach computes accurate funnel estimates far more efficiently and leaves formal verification to the end, outside all funnel size optimization loops.

Convergent Approximate Solving of First-Order Constraints by Approximate Quantifiers

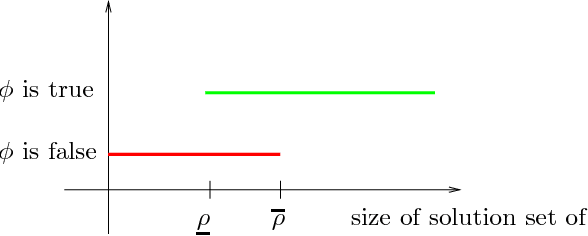
Exactly solving first-order constraints (i.e., first-order formulas over a certain predefined structure) can be a very hard, or even undecidable problem. In continuous structures like the real numbers it is promising to compute approximate solutions instead of exact ones. However, the quantifiers of the first-order predicate language are an obstacle to allowing approximations to arbitrary small error bounds. In this paper we solve the problem by modifying the first-order language and replacing the classical quantifiers with approximate quantifiers. These also have two additional advantages: First, they are tunable, in the sense that they allow the user to decide on the trade-off between precision and efficiency. Second, they introduce additional expressivity into the first-order language by allowing reasoning over the size of solution sets.

Solving Composed First-Order Constraints from Discrete-Time Robust Control

This paper deals with a problem from discrete-time robust control which requires the solution of constraints over the reals that contain both universal and existential quantifiers. For solving this problem we formulate it as a program in a (fictitious) constraint logic programming language with explicit quantifier notation. This allows us to clarify the special structure of the problem, and to extend an algorithm for computing approximate solution sets of first-order constraints over the reals to exploit this structure. As a result we can deal with inputs that are clearly out of reach for current symbolic solvers.