Convergent Approximate Solving of First-Order Constraints by Approximate Quantifiers
Paper and Code
Dec 20, 2002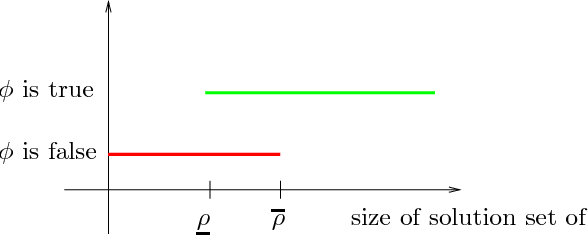
Exactly solving first-order constraints (i.e., first-order formulas over a certain predefined structure) can be a very hard, or even undecidable problem. In continuous structures like the real numbers it is promising to compute approximate solutions instead of exact ones. However, the quantifiers of the first-order predicate language are an obstacle to allowing approximations to arbitrary small error bounds. In this paper we solve the problem by modifying the first-order language and replacing the classical quantifiers with approximate quantifiers. These also have two additional advantages: First, they are tunable, in the sense that they allow the user to decide on the trade-off between precision and efficiency. Second, they introduce additional expressivity into the first-order language by allowing reasoning over the size of solution sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge