Stefan Pricopie
An adaptive approach to Bayesian Optimization with switching costs
May 14, 2024


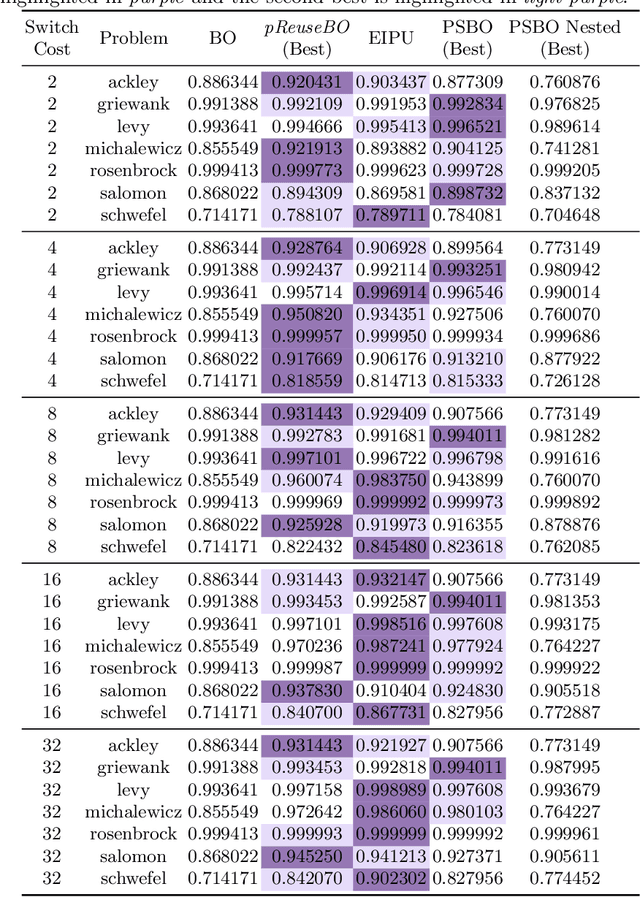
Abstract:We investigate modifications to Bayesian Optimization for a resource-constrained setting of sequential experimental design where changes to certain design variables of the search space incur a switching cost. This models the scenario where there is a trade-off between evaluating more while maintaining the same setup, or switching and restricting the number of possible evaluations due to the incurred cost. We adapt two process-constrained batch algorithms to this sequential problem formulation, and propose two new methods: one cost-aware and one cost-ignorant. We validate and compare the algorithms using a set of 7 scalable test functions in different dimensionalities and switching-cost settings for 30 total configurations. Our proposed cost-aware hyperparameter-free algorithm yields comparable results to tuned process-constrained algorithms in all settings we considered, suggesting some degree of robustness to varying landscape features and cost trade-offs. This method starts to outperform the other algorithms with increasing switching-cost. Our work broadens out from other recent Bayesian Optimization studies in resource-constrained settings that consider a batch setting only. While the contributions of this work are relevant to the general class of resource-constrained problems, they are particularly relevant to problems where adaptability to varying resource availability is of high importance
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge