Nonlocal Neural Tangent Kernels via Parameter-Space Interactions

The Neural Tangent Kernel (NTK) framework has provided deep insights into the training dynamics of neural networks under gradient flow. However, it relies on the assumption that the network is differentiable with respect to its parameters, an assumption that breaks down when considering non-smooth target functions or parameterized models exhibiting non-differentiable behavior. In this work, we propose a Nonlocal Neural Tangent Kernel (NNTK) that replaces the local gradient with a nonlocal interaction-based approximation in parameter space. Nonlocal gradients are known to exist for a wider class of functions than the standard gradient. This allows NTK theory to be extended to nonsmooth functions, stochastic estimators, and broader families of models. We explore both fixed-kernel and attention-based formulations of this nonlocal operator. We illustrate the new formulation with numerical studies.

Physics Informed Machine Learning (PIML) methods for estimating the remaining useful lifetime (RUL) of aircraft engines

This paper is aimed at using the newly developing field of physics informed machine learning (PIML) to develop models for predicting the remaining useful lifetime (RUL) aircraft engines. We consider the well-known benchmark NASA Commercial Modular Aero-Propulsion System Simulation (C-MAPSS) data as the main data for this paper, which consists of sensor outputs in a variety of different operating modes. C-MAPSS is a well-studied dataset with much existing work in the literature that address RUL prediction with classical and deep learning methods. In the absence of published empirical physical laws governing the C-MAPSS data, our approach first uses stochastic methods to estimate the governing physics models from the noisy time series data. In our approach, we model the various sensor readings as being governed by stochastic differential equations, and we estimate the corresponding transition density mean and variance functions of the underlying processes. We then augment LSTM (long-short term memory) models with the learned mean and variance functions during training and inferencing. Our PIML based approach is different from previous methods, and we use the data to first learn the physics. Our results indicate that PIML discovery and solutions methods are well suited for this problem and outperform previous data-only deep learning methods for this data set and task. Moreover, the framework developed herein is flexible, and can be adapted to other situations (other sensor modalities or combined multi-physics environments), including cases where the underlying physics is only partially observed or known.

Marrying Compressed Sensing and Deep Signal Separation

Blind signal separation (BSS) is an important and challenging signal processing task. Given an observed signal which is a superposition of a collection of unknown (hidden/latent) signals, BSS aims at recovering the separate, underlying signals from only the observed mixed signal. As an underdetermined problem, BSS is notoriously difficult to solve in general, and modern deep learning has provided engineers with an effective set of tools to solve this problem. For example, autoencoders learn a low-dimensional hidden encoding of the input data which can then be used to perform signal separation. In real-time systems, a common bottleneck is the transmission of data (communications) to a central command in order to await decisions. Bandwidth limits dictate the frequency and resolution of the data being transmitted. To overcome this, compressed sensing (CS) technology allows for the direct acquisition of compressed data with a near optimal reconstruction guarantee. This paper addresses the question: can compressive acquisition be combined with deep learning for BSS to provide a complete acquire-separate-predict pipeline? In other words, the aim is to perform BSS on a compressively acquired signal directly without ever having to decompress the signal. We consider image data (MNIST and E-MNIST) and show how our compressive autoencoder approach solves the problem of compressive BSS. We also provide some theoretical insights into the problem.

BrowNNe: Brownian Nonlocal Neurons & Activation Functions

It is generally thought that the use of stochastic activation functions in deep learning architectures yield models with superior generalization abilities. However, a sufficiently rigorous statement and theoretical proof of this heuristic is lacking in the literature. In this paper, we provide several novel contributions to the literature in this regard. Defining a new notion of nonlocal directional derivative, we analyze its theoretical properties (existence and convergence). Second, using a probabilistic reformulation, we show that nonlocal derivatives are epsilon-sub gradients, and derive sample complexity results for convergence of stochastic gradient descent-like methods using nonlocal derivatives. Finally, using our analysis of the nonlocal gradient of Holder continuous functions, we observe that sample paths of Brownian motion admit nonlocal directional derivatives, and the nonlocal derivatives of Brownian motion are seen to be Gaussian processes with computable mean and standard deviation. Using the theory of nonlocal directional derivatives, we solve a highly nondifferentiable and nonconvex model problem of parameter estimation on image articulation manifolds. Using Brownian motion infused ReLU activation functions with the nonlocal gradient in place of the usual gradient during backpropagation, we also perform experiments on multiple well-studied deep learning architectures. Our experiments indicate the superior generalization capabilities of Brownian neural activation functions in low-training data regimes, where the use of stochastic neurons beats the deterministic ReLU counterpart.

A Theory for Optical flow-based Transport on Image Manifolds

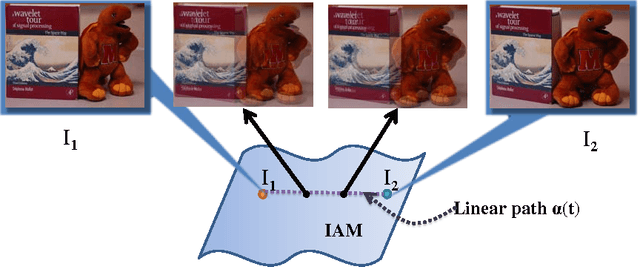
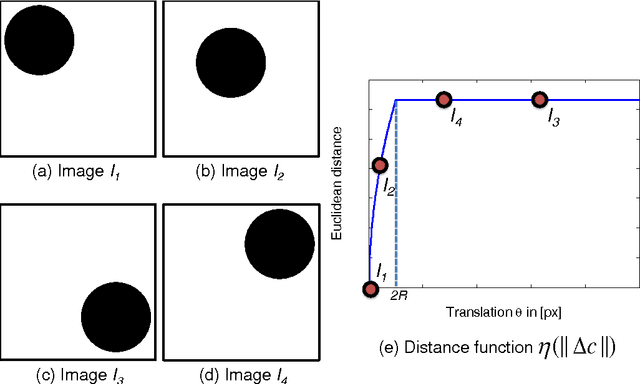
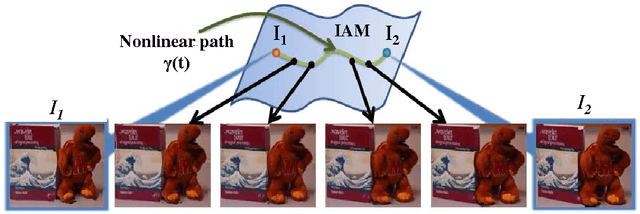
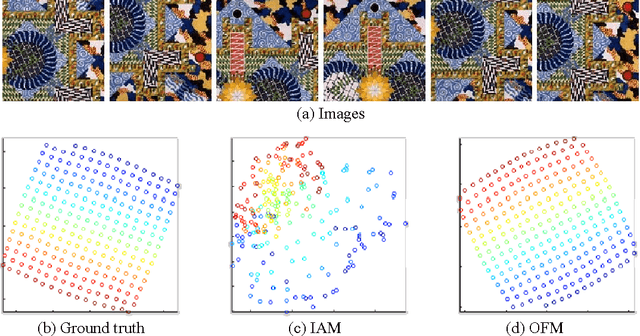
An image articulation manifold (IAM) is the collection of images formed when an object is articulated in front of a camera. IAMs arise in a variety of image processing and computer vision applications, where they provide a natural low-dimensional embedding of the collection of high-dimensional images. To date IAMs have been studied as embedded submanifolds of Euclidean spaces. Unfortunately, their promise has not been realized in practice, because real world imagery typically contains sharp edges that render an IAM non-differentiable and hence non-isometric to the low-dimensional parameter space under the Euclidean metric. As a result, the standard tools from differential geometry, in particular using linear tangent spaces to transport along the IAM, have limited utility. In this paper, we explore a nonlinear transport operator for IAMs based on the optical flow between images and develop new analytical tools reminiscent of those from differential geometry using the idea of optical flow manifolds (OFMs). We define a new metric for IAMs that satisfies certain local isometry conditions, and we show how to use this metric to develop a new tools such as flow fields on IAMs, parallel flow fields, parallel transport, as well as a intuitive notion of curvature. The space of optical flow fields along a path of constant curvature has a natural multi-scale structure via a monoid structure on the space of all flow fields along a path. We also develop lower bounds on approximation errors while approximating non-parallel flow fields by parallel flow fields.