A Theory for Optical flow-based Transport on Image Manifolds
Paper and Code
Nov 22, 2011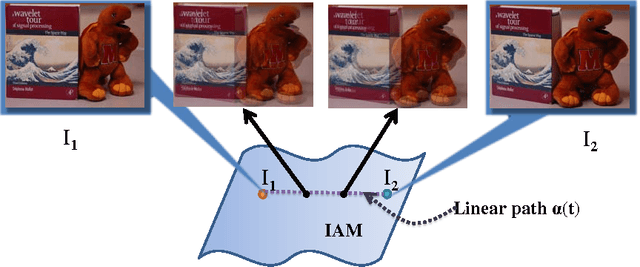
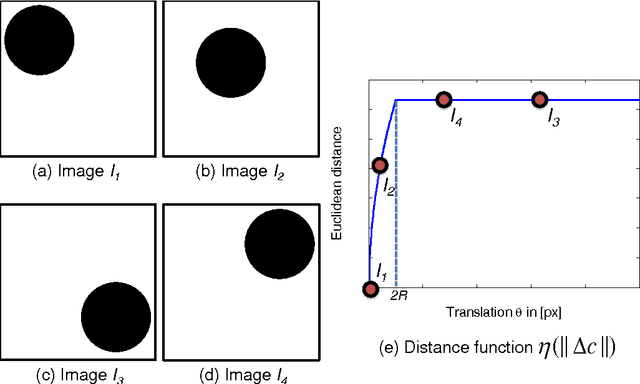
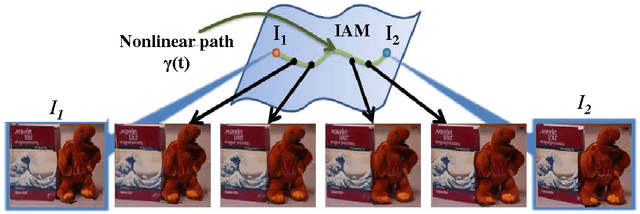
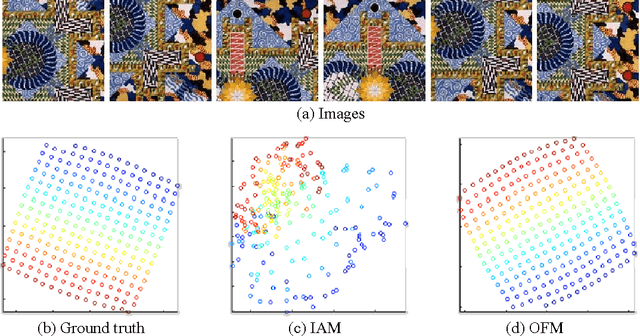
An image articulation manifold (IAM) is the collection of images formed when an object is articulated in front of a camera. IAMs arise in a variety of image processing and computer vision applications, where they provide a natural low-dimensional embedding of the collection of high-dimensional images. To date IAMs have been studied as embedded submanifolds of Euclidean spaces. Unfortunately, their promise has not been realized in practice, because real world imagery typically contains sharp edges that render an IAM non-differentiable and hence non-isometric to the low-dimensional parameter space under the Euclidean metric. As a result, the standard tools from differential geometry, in particular using linear tangent spaces to transport along the IAM, have limited utility. In this paper, we explore a nonlinear transport operator for IAMs based on the optical flow between images and develop new analytical tools reminiscent of those from differential geometry using the idea of optical flow manifolds (OFMs). We define a new metric for IAMs that satisfies certain local isometry conditions, and we show how to use this metric to develop a new tools such as flow fields on IAMs, parallel flow fields, parallel transport, as well as a intuitive notion of curvature. The space of optical flow fields along a path of constant curvature has a natural multi-scale structure via a monoid structure on the space of all flow fields along a path. We also develop lower bounds on approximation errors while approximating non-parallel flow fields by parallel flow fields.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge