C2W-Tune: Cavity-to -Wall Transfer Learning for Thin Atrial Wall Segmentation in 3D Late Gadolinium-enhanced Magnetic Resonance

Accurate segmentation of the left atrial (LA) wall in 3D late gadolinium-enhanced MRI (LGE-MRI) is essential for wall thickness mapping and fibrosis quantification, yet it remains challenging due to the wall's thinness, complex anatomy, and low contrast. We propose C2W-Tune, a two-stage cavity-to-wall transfer framework that leverages a high-accuracy LA cavity model as an anatomical prior to improve thin-wall delineation. Using a 3D U-Net with a ResNeXt encoder and instance normalization, Stage 1 pre-trains the network to segment the LA cavity, learning robust atrial representations. Stage 2 transfers these weights and adapts the network to LA wall segmentation using a progressive layer-unfreezing schedule to preserve endocardial features while enabling wall-specific refinement. Experiments on the 2018 LA Segmentation Challenge dataset demonstrate substantial gains over an architecture-matched baseline trained from scratch: wall Dice improves from 0.623 to 0.814, and Surface Dice at 1 mm improves from 0.553 to 0.731. Boundary errors were substantially reduced, with the 95th-percentile Hausdorff distance (HD95) decreasing from 2.95 mm to 2.55 mm and the average symmetric surface distance (ASSD) from 0.71 mm to 0.63 mm. Furthermore, even with reduced supervision (70 training volumes sampled from the same training pool), C2W-Tune achieved a Dice score of 0.78 and an HD95 of 3.15 mm, maintaining competitive performance and exceeding multi-class benchmarks that typically report Dice values around 0.6-0.7. These results show that anatomically grounded task transfer with controlled fine-tuning improves boundary accuracy for thin LA wall segmentation in 3D LGE-MRI.

Few-Shot Left Atrial Wall Segmentation in 3D LGE MRI via Meta-Learning

Segmenting the left atrial wall from late gadolinium enhancement magnetic resonance images (MRI) is challenging due to the wall's thin geometry, low contrast, and the scarcity of expert annotations. We propose a Model-Agnostic Meta-Learning (MAML) framework for K-shot (K = 5, 10, 20) 3D left atrial wall segmentation that is meta-trained on the wall task together with auxiliary left atrial and right atrial cavity tasks and uses a boundary-aware composite loss to emphasize thin-structure accuracy. We evaluated MAML segmentation performance on a hold-out test set and assessed robustness under an unseen synthetic shift and on a distinct local cohort. On the hold-out test set, MAML appeared to improve segmentation performance compared to the supervised fine-tuning model, achieving a Dice score (DSC) of 0.64 vs. 0.52 and HD95 of 5.70 vs. 7.60 mm at 5-shot, and approached the fully supervised reference at 20-shot (0.69 vs. 0.71 DSC). Under unseen shift, performance degraded but remained robust: at 5-shot, MAML attained 0.59 DSC and 5.99 mm HD95 on the unseen domain shift and 0.57 DSC and 6.01 mm HD95 on the local cohort, with consistent gains as K increased. These results suggest that more accurate and reliable thin-wall boundaries are achievable in low-shot adaptation, potentially enabling clinical translation with minimal additional labeling for the assessment of atrial remodeling.

3D Conditional Image Synthesis of Left Atrial LGE MRI from Composite Semantic Masks

Segmentation of the left atrial (LA) wall and endocardium from late gadolinium-enhanced (LGE) MRI is essential for quantifying atrial fibrosis in patients with atrial fibrillation. The development of accurate machine learning-based segmentation models remains challenging due to the limited availability of data and the complexity of anatomical structures. In this work, we investigate 3D conditional generative models as potential solution for augmenting scarce LGE training data and improving LA segmentation performance. We develop a pipeline to synthesize high-fidelity 3D LGE MRI volumes from composite semantic label maps combining anatomical expert annotations with unsupervised tissue clusters, using three 3D conditional generators (Pix2Pix GAN, SPADE-GAN, and SPADE-LDM). The synthetic images are evaluated for realism and their impact on downstream LA segmentation. SPADE-LDM generates the most realistic and structurally accurate images, achieving an FID of 4.063 and surpassing GAN models, which have FIDs of 40.821 and 7.652 for Pix2Pix and SPADE-GAN, respectively. When augmented with synthetic LGE images, the Dice score for LA cavity segmentation with a 3D U-Net model improved from 0.908 to 0.936, showing a statistically significant improvement (p < 0.05) over the baseline.These findings demonstrate the potential of label-conditioned 3D synthesis to enhance the segmentation of under-represented cardiac structures.

Noise-Type Radars: Probability of Detection vs. Correlation Coefficient and Integration Time

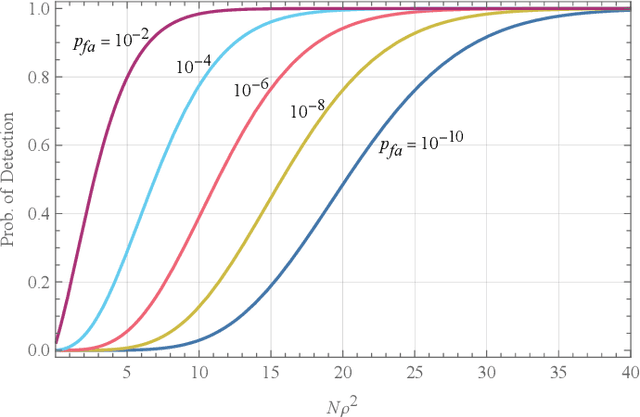
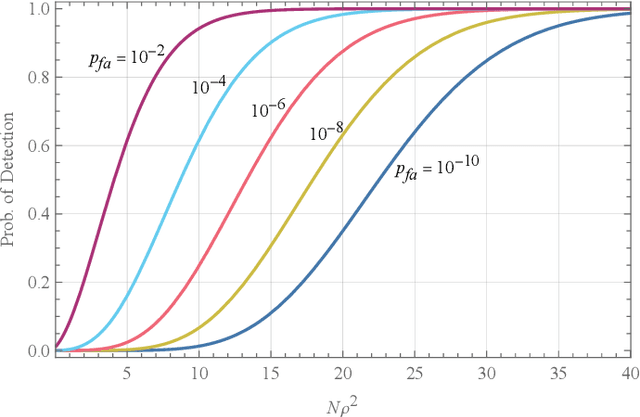
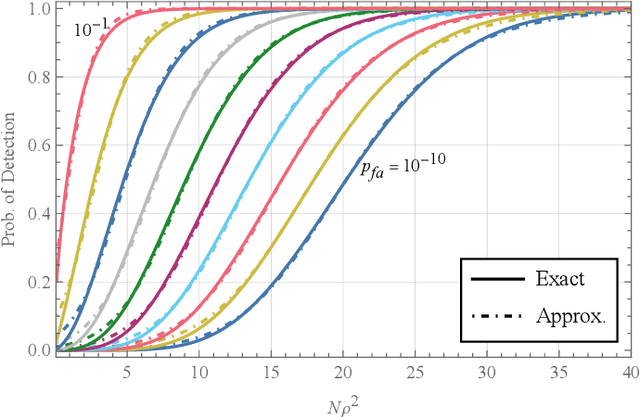
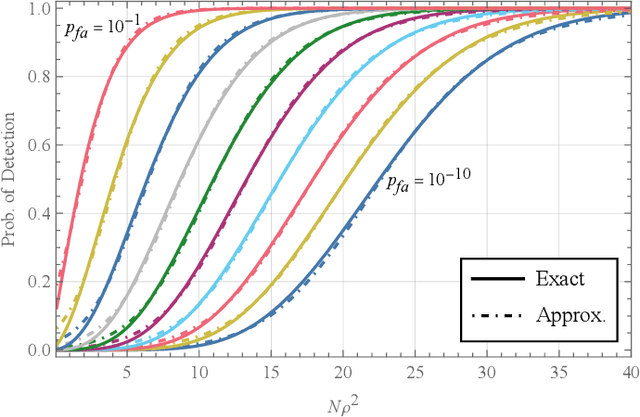
Noise radars have the same mathematical description as a type of quantum radar known as quantum two-mode squeezing radar. Although their physical implementations are very different, this mathematical similarity allows us to analyze them collectively. We may consider the two types of radars as forming a single class of radars, called noise-type radars. The target detection performance of noise-type radars depends on two parameters: the number of integrated samples and a correlation coefficient. In this paper, we show that when the number of integrated samples is large and the correlation coefficient is low, the detection performance becomes a function of a single parameter: the number of integrated samples multiplied by the square of the correlation coefficient. We then explore the detection performance of noise-type radars in terms of this emergent parameter; in particular, we determine the probability of detection as a function of this parameter.

Structured Covariance Matrix Estimation for Noise-Type Radars

Standard noise radars, as well as noise-type radars such as quantum two-mode squeezing radar, are characterized by a covariance matrix with a very specific structure. This matrix has four independent parameters: the amplitude of the received signal, the amplitude of the internal signal used for matched filtering, the correlation between the two signals, and the relative phase between them. In this paper, we derive estimators for these four parameters using two techniques. The first is based on minimizing the Frobenius norm between the structured covariance matrix and the sample covariance matrix; the second is maximum likelihood parameter estimation. The two techniques yield the same estimators. We then give probability density functions (PDFs) for all four estimators. Because some of these PDFs are quite complicated, we also provide approximate PDFs. Finally, we apply our results to the problem of target detection and derive expressions for the receiver operating characteristic curves of two different noise radar detectors.

A Family of Neyman-Pearson-Based Detectors for Noise-Type Radars

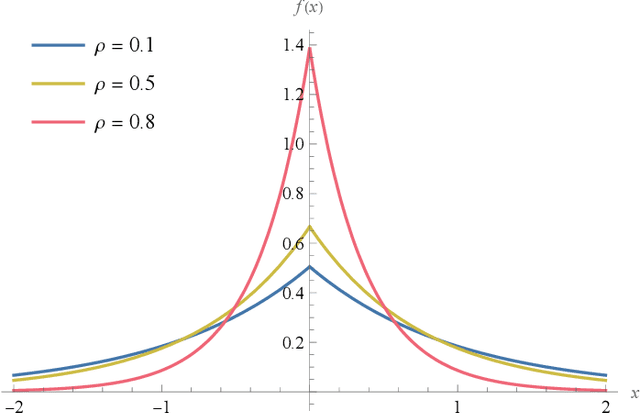
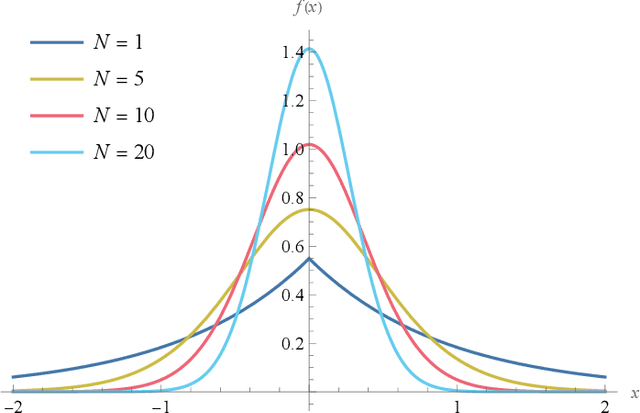
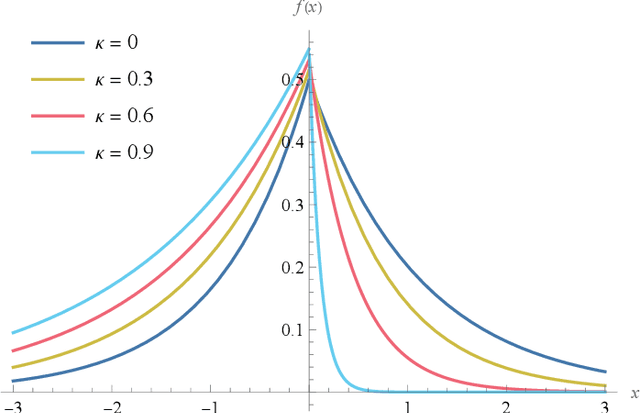
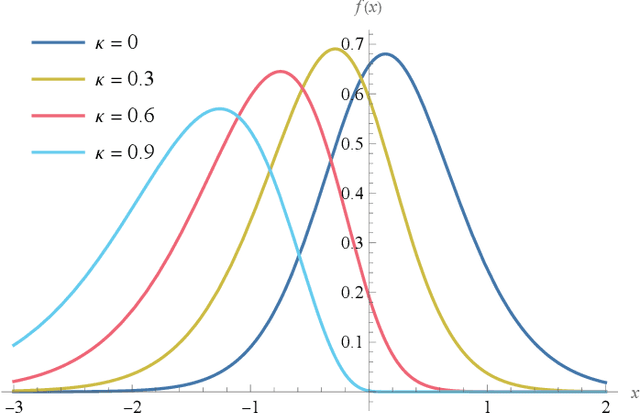
We derive a detector that optimizes the target detection performance of any single-input single-output noise radar satisfying the following properties: it transmits Gaussian noise, it retains an internal reference signal for matched filtering, all external noise is additive white Gaussian noise, and all signals are measured using heterodyne receivers. This class of radars, which we call noise-type radars, includes not only many types of standard noise radars, but also a type of quantum radar known as quantum two-mode squeezing radar. The detector, which we derive using the Neyman-Pearson lemma, is not practical because it requires foreknowledge of a target-dependent correlation coefficient that cannot be known beforehand. (It is, however, a natural standard of comparison for other detectors.) This motivates us to study the family of Neyman-Pearson-based detectors that result when the correlation coefficient is treated as a parameter. We derive the probability distribution of the Neyman-Pearson-based detectors when there is a mismatch between the pre-chosen parameter value and the true correlation coefficient. We then use this result to generate receiver operating characteristic curves. Finally, we apply our results to the case where the correlation coefficient is small. It turns out that the resulting detector is not only a good one, but that it has appeared previously in the quantum radar literature.

Faster Maximum Feasible Subsystem Solutions for Dense Constraint Matrices

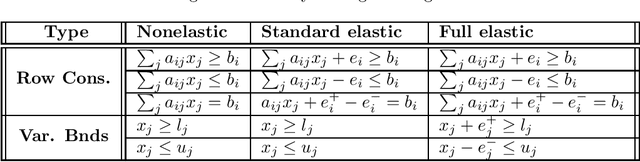
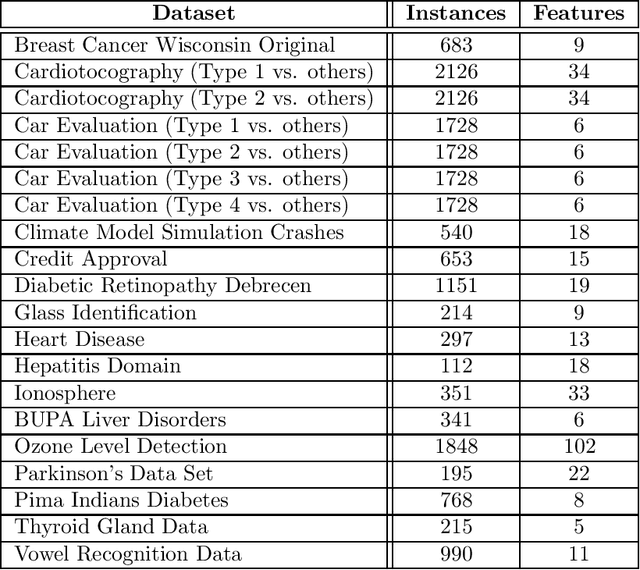
Finding the largest cardinality feasible subset of an infeasible set of linear constraints is the Maximum Feasible Subsystem problem (MAX FS). Solving this problem is crucial in a wide range of applications such as machine learning and compressive sensing. Although MAX FS is NP-hard, useful heuristic algorithms exist, but these can be slow for large problems. We extend the existing heuristics for the case of dense constraint matrices to greatly increase their speed while preserving or improving solution quality. We test the extended algorithms on two applications that have dense constraint matrices: binary classification, and sparse recovery in compressive sensing. In both cases, speed is greatly increased with no loss of accuracy.