A Family of Neyman-Pearson-Based Detectors for Noise-Type Radars
Paper and Code
Apr 16, 2022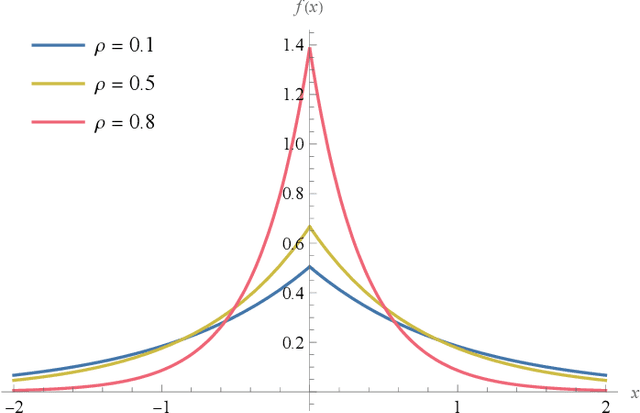
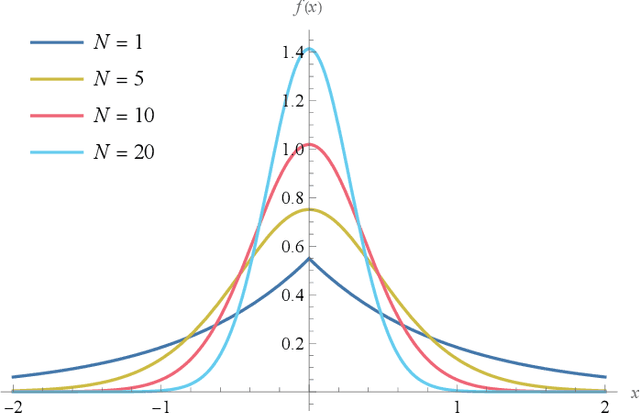
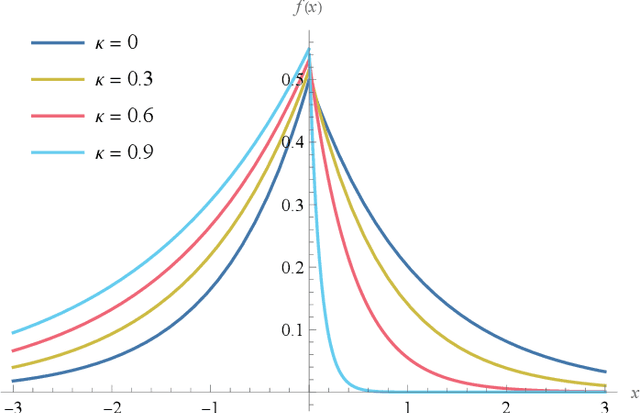
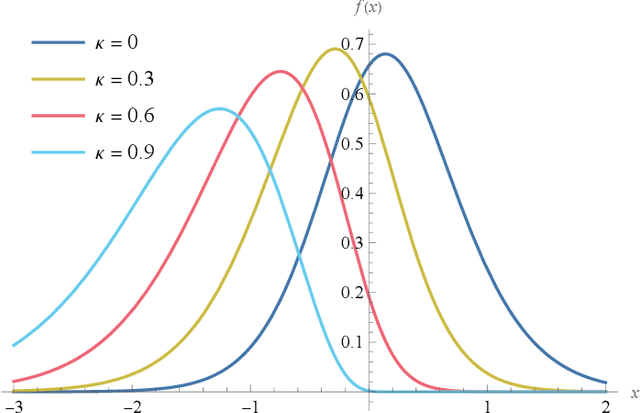
We derive a detector that optimizes the target detection performance of any single-input single-output noise radar satisfying the following properties: it transmits Gaussian noise, it retains an internal reference signal for matched filtering, all external noise is additive white Gaussian noise, and all signals are measured using heterodyne receivers. This class of radars, which we call noise-type radars, includes not only many types of standard noise radars, but also a type of quantum radar known as quantum two-mode squeezing radar. The detector, which we derive using the Neyman-Pearson lemma, is not practical because it requires foreknowledge of a target-dependent correlation coefficient that cannot be known beforehand. (It is, however, a natural standard of comparison for other detectors.) This motivates us to study the family of Neyman-Pearson-based detectors that result when the correlation coefficient is treated as a parameter. We derive the probability distribution of the Neyman-Pearson-based detectors when there is a mismatch between the pre-chosen parameter value and the true correlation coefficient. We then use this result to generate receiver operating characteristic curves. Finally, we apply our results to the case where the correlation coefficient is small. It turns out that the resulting detector is not only a good one, but that it has appeared previously in the quantum radar literature.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge