Faster Maximum Feasible Subsystem Solutions for Dense Constraint Matrices
Paper and Code
Feb 10, 2021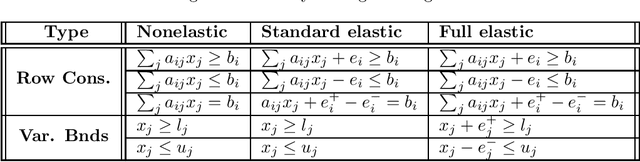


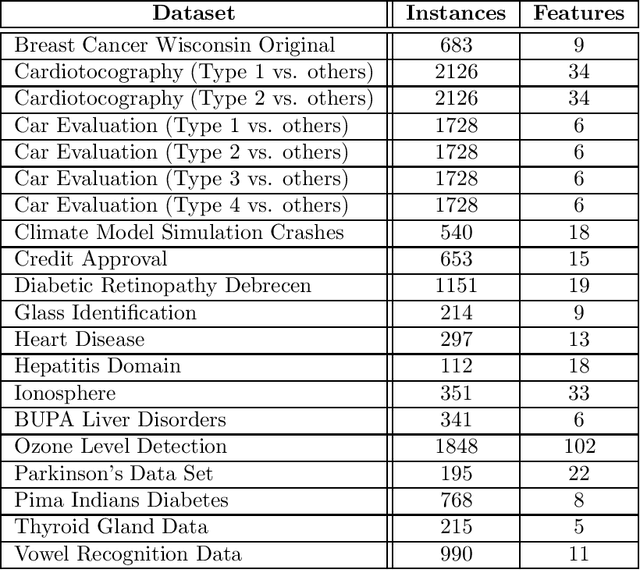
Finding the largest cardinality feasible subset of an infeasible set of linear constraints is the Maximum Feasible Subsystem problem (MAX FS). Solving this problem is crucial in a wide range of applications such as machine learning and compressive sensing. Although MAX FS is NP-hard, useful heuristic algorithms exist, but these can be slow for large problems. We extend the existing heuristics for the case of dense constraint matrices to greatly increase their speed while preserving or improving solution quality. We test the extended algorithms on two applications that have dense constraint matrices: binary classification, and sparse recovery in compressive sensing. In both cases, speed is greatly increased with no loss of accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge