Uncovering delayed patterns in noisy and irregularly sampled time series: an astronomy application

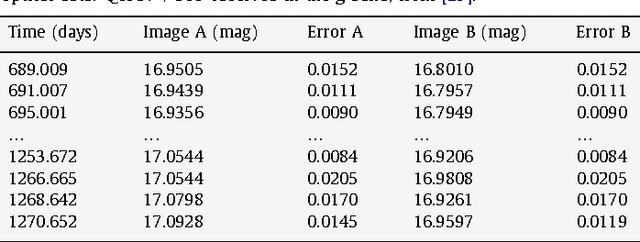
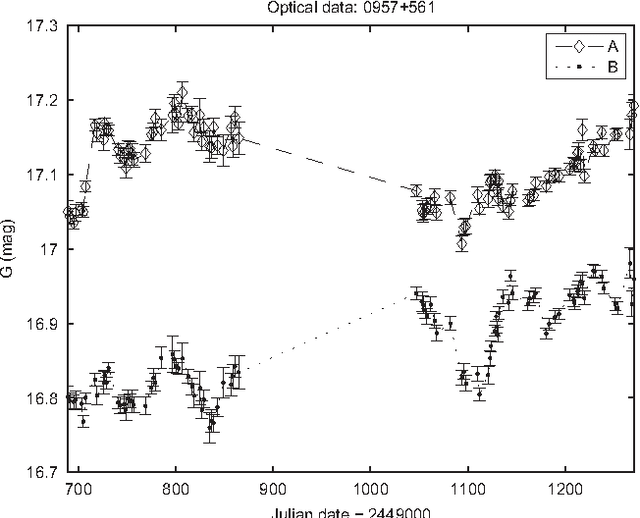
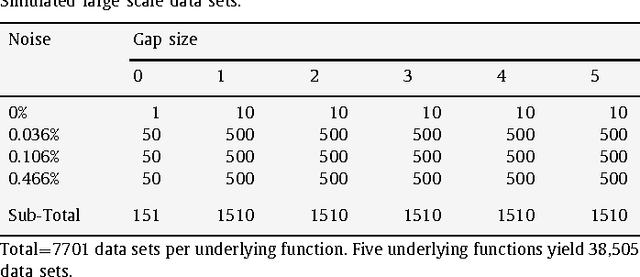
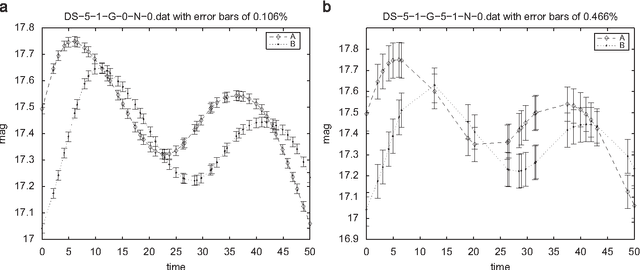
We study the problem of estimating the time delay between two signals representing delayed, irregularly sampled and noisy versions of the same underlying pattern. We propose and demonstrate an evolutionary algorithm for the (hyper)parameter estimation of a kernel-based technique in the context of an astronomical problem, namely estimating the time delay between two gravitationally lensed signals from a distant quasar. Mixed types (integer and real) are used to represent variables within the evolutionary algorithm. We test the algorithm on several artificial data sets, and also on real astronomical observations of quasar Q0957+561. By carrying out a statistical analysis of the results we present a detailed comparison of our method with the most popular methods for time delay estimation in astrophysics. Our method yields more accurate and more stable time delay estimates: for Q0957+561, we obtain 419.6 days for the time delay between images A and B. Our methodology can be readily applied to current state-of-the-art optical monitoring data in astronomy, but can also be applied in other disciplines involving similar time series data.

How accurate are the time delay estimates in gravitational lensing?

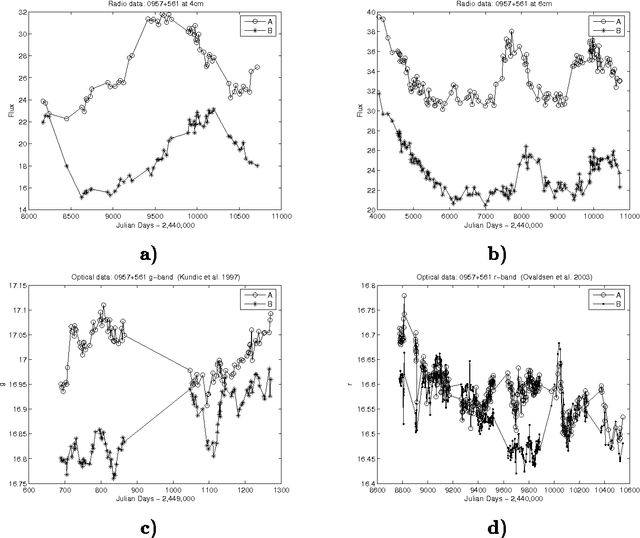
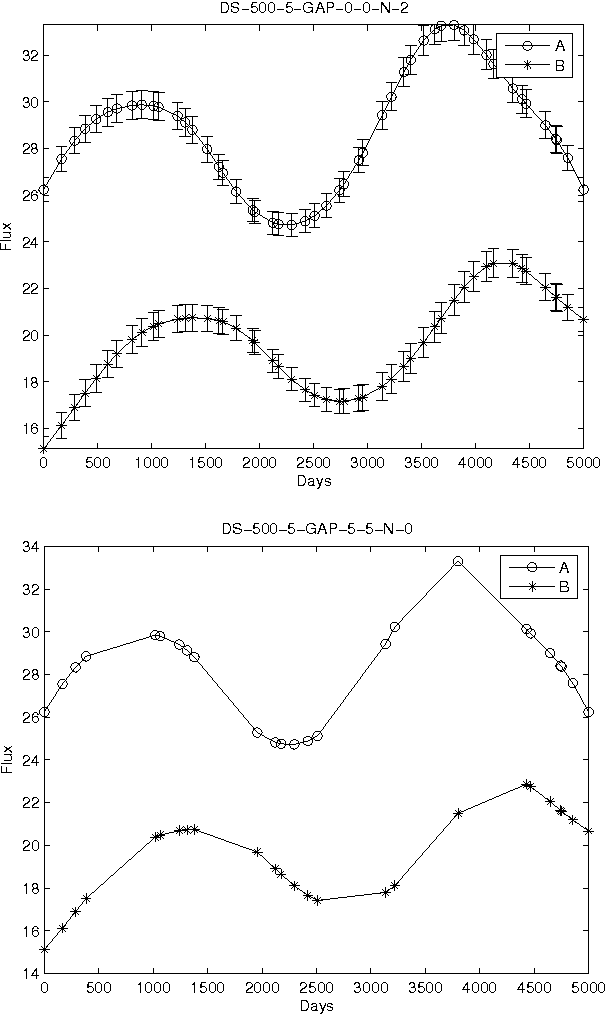
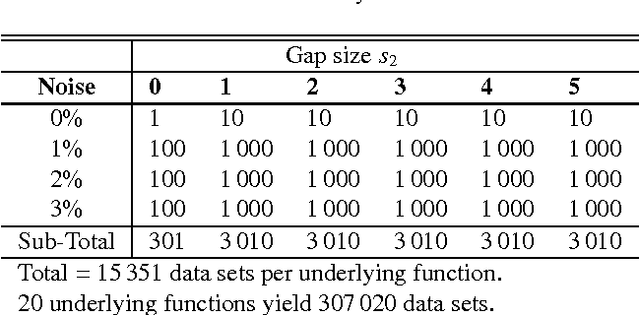
We present a novel approach to estimate the time delay between light curves of multiple images in a gravitationally lensed system, based on Kernel methods in the context of machine learning. We perform various experiments with artificially generated irregularly-sampled data sets to study the effect of the various levels of noise and the presence of gaps of various size in the monitoring data. We compare the performance of our method with various other popular methods of estimating the time delay and conclude, from experiments with artificial data, that our method is least vulnerable to missing data and irregular sampling, within reasonable bounds of Gaussian noise. Thereafter, we use our method to determine the time delays between the two images of quasar Q0957+561 from radio monitoring data at 4 cm and 6 cm, and conclude that if only the observations at epochs common to both wavelengths are used, the time delay gives consistent estimates, which can be combined to yield 408\pm 12 days. The full 6 cm dataset, which covers a longer monitoring period, yields a value which is 10% larger, but this can be attributed to differences in sampling and missing data.