Learning in PINNs: Phase transition, total diffusion, and generalization

We investigate the learning dynamics of fully-connected neural networks through the lens of gradient signal-to-noise ratio (SNR), examining the behavior of first-order optimizers like Adam in non-convex objectives. By interpreting the drift/diffusion phases in the information bottleneck theory, focusing on gradient homogeneity, we identify a third phase termed ``total diffusion", characterized by equilibrium in the learning rates and homogeneous gradients. This phase is marked by an abrupt SNR increase, uniform residuals across the sample space and the most rapid training convergence. We propose a residual-based re-weighting scheme to accelerate this diffusion in quadratic loss functions, enhancing generalization. We also explore the information compression phenomenon, pinpointing a significant saturation-induced compression of activations at the total diffusion phase, with deeper layers experiencing negligible information loss. Supported by experimental data on physics-informed neural networks (PINNs), which underscore the importance of gradient homogeneity due to their PDE-based sample inter-dependence, our findings suggest that recognizing phase transitions could refine ML optimization strategies for improved generalization.

Residual-based attention and connection to information bottleneck theory in PINNs

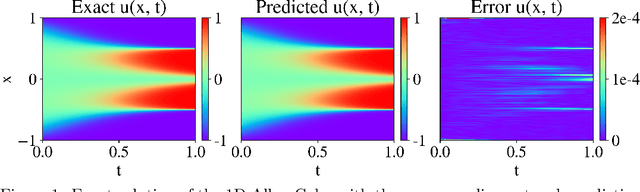
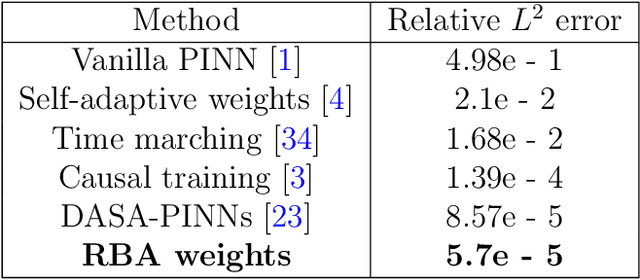
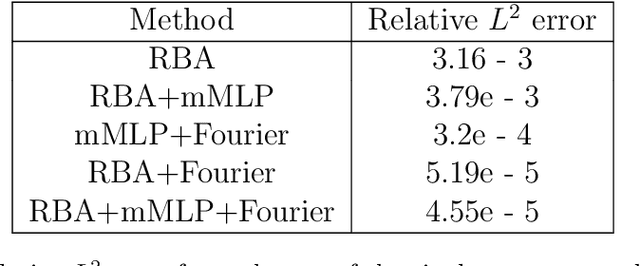
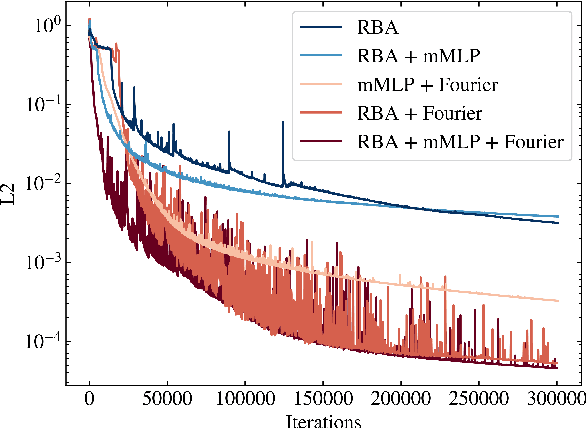
Driven by the need for more efficient and seamless integration of physical models and data, physics-informed neural networks (PINNs) have seen a surge of interest in recent years. However, ensuring the reliability of their convergence and accuracy remains a challenge. In this work, we propose an efficient, gradient-less weighting scheme for PINNs, that accelerates the convergence of dynamic or static systems. This simple yet effective attention mechanism is a function of the evolving cumulative residuals and aims to make the optimizer aware of problematic regions at no extra computational cost or adversarial learning. We illustrate that this general method consistently achieves a relative $L^{2}$ error of the order of $10^{-5}$ using standard optimizers on typical benchmark cases of the literature. Furthermore, by investigating the evolution of weights during training, we identify two distinct learning phases reminiscent of the fitting and diffusion phases proposed by the information bottleneck (IB) theory. Subsequent gradient analysis supports this hypothesis by aligning the transition from high to low signal-to-noise ratio (SNR) with the transition from fitting to diffusion regimes of the adopted weights. This novel correlation between PINNs and IB theory could open future possibilities for understanding the underlying mechanisms behind the training and stability of PINNs and, more broadly, of neural operators.